Mới nhất Ngữ văn IELTS TOEIC Từ vựng tiếng Anh Tiếng Anh giao tiếp Tiếng Anh THPT Kỹ năng tiếng Anh Ngôn ngữ khác

Nội dung bài viết

1. Khái niệm đường tròn nội tiếp tam giác
2. Cách xác định tâm đường tròn nội tiếp tam giác
3. Bán kính đường tròn nội tiếp tam giác
4. Phương trình đường tròn nội tiếp tam giác
5. Các dạng bài tập về đường tròn nội tiếp tam giác
6. Bài tập vận dụng đường tròn nội tiếp tam giác
7. Bài tập tự luyện tâm đường tròn nội tiếp tam giác

Tâm đường tròn nội tiếp tam giác: Lý thuyết chi tiết và bài tập đa dạng dành cho học sinh lớp 9

Chia sẻ

Tâm đường tròn nội tiếp tam giác là một phần kiến thức nền tảng trong Toán học lớp 9, thường xuất hiện trong các đề thi vào lớp 10. Đây là chủ đề quan trọng giúp học sinh nắm vững kỹ năng hình học cơ bản.

Tài liệu về tâm đường tròn nội tiếp tam giác bao gồm toàn bộ lý thuyết và bài tập từ cơ bản đến nâng cao. Nội dung chi tiết hướng dẫn cách xác định tâm, công thức tính toán, phương trình đường tròn nội tiếp, cùng ví dụ minh họa và bài tập tự luyện có đáp án. Qua đó, học sinh có thể hệ thống hóa kiến thức và rèn luyện kỹ năng giải bài tập hiệu quả. Để mở rộng kiến thức, học sinh có thể tham khảo thêm các tài liệu như: chuyên đề Giải phương trình bậc hai chứa tham số, bài tập hệ thức Vi-et và ứng dụng.

1. Khái niệm đường tròn nội tiếp tam giác

a. Đường tròn được định nghĩa là tập hợp tất cả các điểm trên một mặt phẳng cách đều một điểm cố định (gọi là tâm) một khoảng cách không đổi (gọi là bán kính). Ký hiệu đường tròn có tâm O và bán kính r là (O; r).

b. Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó. Ngoài ra, đường tròn nội tiếp còn được gọi là đường tròn được bao quanh bởi tam giác ngoại tiếp.

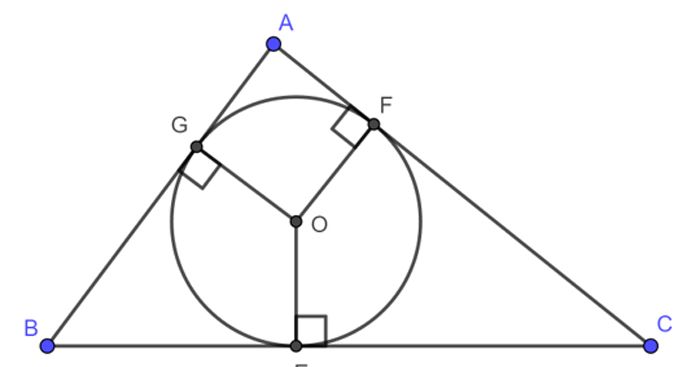
2. Cách xác định tâm đường tròn nội tiếp tam giác

Để xác định tâm đường tròn nội tiếp tam giác, bao gồm cả tam giác vuông và tam giác đều, việc nắm vững lý thuyết là điều cần thiết.

Cách xác định hoặc vẽ tâm đường tròn nội tiếp tam giác rất đơn giản: chỉ cần vẽ hai đường phân giác trong của tam giác. Giao điểm của hai đường phân giác này chính là tâm đường tròn nội tiếp.

Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác trong, hoặc có thể chỉ cần hai đường phân giác.

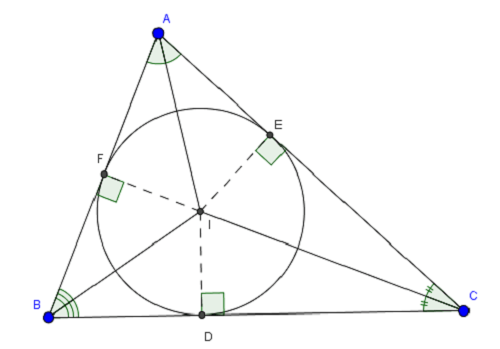
- Cách 1: Gọi D, E, F lần lượt là chân đường phân giác trong của tam giác ABC kẻ từ các đỉnh A, B, C.

+ Bước 1: Tính độ dài các cạnh của tam giác.

$k_{1} = \frac{AB}{AC}, k_{2} = \frac{BA}{BC}, k_{3}=\frac{CA}{CB}$

k_{1} = \frac{A B}{A C}, k_{2} = \frac{B A}{B C}, k_{3} = \frac{C A}{C B}

+ Bước 3: Tìm tọa độ các điểm D, E, F.

+ Bước 4: Viết phương trình đường thẳng AD và BE.

+ Bước 5: Tâm đường tròn nội tiếp tam giác ABC là giao điểm của AD và BE.

- Cách 2: Trong mặt phẳng Oxy, tọa độ điểm I có thể được xác định như sau:

$\left\{\begin{matrix} x_{I} = \frac{BC.x_{A} + CA.x_{B} + AB.x_{C}}{BC+CA+AB}\\ y_{I} = \frac{BC.y_{A}+CA.y_{B}+AB.y_{C}}{BC+AC+BC} \end{matrix}\right.$

{\begin{matrix} x_{I} = \frac{B C . x_{A} + C A . x_{B} + A B . x_{C}}{B C + C A + A B} \\ y_{I} = \frac{B C . y_{A} + C A . y_{B} + A B . y_{C}}{B C + A C + B C} \end{matrix}

Cách 3

Để xác định đường tròn tâm I nội tiếp tam giác MNP, chúng ta thực hiện các bước sau:

Bước 1: Vẽ ba đường phân giác trong của tam giác MNP, lần lượt là MD, NE và PF.

Bước 2: Xác định giao điểm I của ba đường phân giác trong tam giác MNP.

Bước 3: Từ tâm I, kẻ ba đường vuông góc với ba cạnh MN, MP và NP của tam giác MNP. Giao điểm của ba đường phân giác chính là tâm I của đường tròn nội tiếp tam giác MNP.

Bước 4: Vẽ đường tròn tâm I với bán kính IF = IE = ID.

Một số trường hợp đặc biệt khi xác định đường tròn nội tiếp tam giác: đường tròn nội tiếp tam giác vuông, tam giác cân và tam giác đều.

3. Bán kính đường tròn nội tiếp tam giác

Tam giác ABC với độ dài ba cạnh lần lượt là a, b, c tương ứng với các cạnh BC, AC, và AB.

- Nửa chu vi của tam giác

$p = \dfrac {a+b+c} {2}$

p = \frac{a + b + c}{2}

- Bán kính đường tròn nội tiếp tam giác

$r = \dfrac {2S}{a+b+c} =\sqrt{\dfrac {(p-a)(p-b)(p-c)}{p}}$

r = \frac{2 S}{a + b + c} = \sqrt{\frac{(p - a) (p - b) (p - c)}{p}}

4. Phương trình đường tròn nội tiếp tam giác

- Nhắc lại kiến thức cơ bản:

${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}$

{(x - a)}^{2} + {(y - b)}^{2} = R^{2}

$\left\{ {\begin{array}{*{20}{c}} {\left( {{d_1}} \right):ax + by + c = 0} \\ {\left( {{d_2}} \right):a$

{\begin{matrix} (d_{1}) : a x + b y + c = 0 \\ (d_{2}) : a^{'} x + b^{'} y + c^{'} = 0 \end{matrix}

$\frac{{ax + by + c}}{{\sqrt {{a^2} + {b^2}} }} = \pm \frac{{a$

\frac{a x + b y + c}{\sqrt{a^{2} + b^{2}}} = \pm \frac{a^{'} x + b^{'} y + c^{'}}{\sqrt{a^{' 2} + b^{' 2}}}

$A(x_{A};y_{A}), B(x_{B}; y_{B}), C(x_{C}; y_{C})$

A (x_{A}; y_{A}), B (x_{B}; y_{B}), C (x_{C}; y_{C})

- Phương pháp 1:

+ Xác định phương trình hai đường phân giác của góc A và B

+ Tìm tâm I là giao điểm của hai đường phân giác này

+ Tính bán kính bằng khoảng cách từ I đến một cạnh của tam giác

+ Viết phương trình đường tròn nội tiếp

- Phương pháp 2:

+ Xác định phương trình đường phân giác trong của đỉnh A

+ Tìm tọa độ chân đường phân giác trong đỉnh A

$\underset{ID}{\rightarrow}=- \frac{BD}{BA}\underset{IA}{\rightarrow}$

\underset{I D}{\to} = - \frac{B D}{B A} \underset{I A}{\to}

+ Tính khoảng cách từ tâm I đến một cạnh của tam giác

+ Viết phương trình đường tròn nội tiếp

5. Các dạng bài tập về đường tròn nội tiếp tam giác

Dạng 1: Tìm tâm của đường tròn nội tiếp khi biết tọa độ ba đỉnh

Ví dụ: Trong mặt phẳng Oxy, cho tam giác ABC với các đỉnh A(1;5), B(–4;–5) và C(4;-1). Hãy xác định tâm I của đường tròn nội tiếp tam giác ABC.

Giải:

$AB = 5\sqrt{5}, AC=3\sqrt{5}, BC=4\sqrt{5}$

A B = 5 \sqrt{5}, A C = 3 \sqrt{5}, B C = 4 \sqrt{5}

Do đó:

$\left\{\begin{matrix} x_{I} = \frac{BC.x_{A} + CA.x_{B} + AB.x_{C}}{BC+CA+AB} = \frac{4\sqrt{5}.1 + 3\sqrt{5}.(-4)+5\sqrt{5}.4}{4\sqrt{5}+3\sqrt{5}+5\sqrt{5}} = 1\\ y_{I} = \frac{BC.y_{A}+CA.y_{B}+AB.y_{C}}{BC+AC+BC} = \frac{4\sqrt{5}.5 + 3\sqrt{5}.(-5)+5\sqrt{5}.(-1)}{4\sqrt{5}+3\sqrt{5}+5\sqrt{5}}=0\end{matrix}\right.$

{\begin{matrix} x_{I} = \frac{B C . x_{A} + C A . x_{B} + A B . x_{C}}{B C + C A + A B} = \frac{4 \sqrt{5} .1 + 3 \sqrt{5} . (- 4) + 5 \sqrt{5} .4}{4 \sqrt{5} + 3 \sqrt{5} + 5 \sqrt{5}} = 1 \\ y_{I} = \frac{B C . y_{A} + C A . y_{B} + A B . y_{C}}{B C + A C + B C} = \frac{4 \sqrt{5} .5 + 3 \sqrt{5} . (- 5) + 5 \sqrt{5} . (- 1)}{4 \sqrt{5} + 3 \sqrt{5} + 5 \sqrt{5}} = 0 \end{matrix}

Vậy tâm của đường tròn nội tiếp tam giác ABC là I(1;0)

Dạng 2: Tìm bán kính đường tròn nội tiếp tam giác

Ví dụ: Trong mặt phẳng Oxy, cho tam giác ABC với các đỉnh A(2;6), B(-3;-4), C(5;0). Hãy tìm bán kính đường tròn ngoại tiếp tam giác ABC.

Giải:

$AB=5\sqrt{5}, AC=3\sqrt{5}, BC=4\sqrt{5}$

A B = 5 \sqrt{5}, A C = 3 \sqrt{5}, B C = 4 \sqrt{5}

$p=\frac{AB+AC+BC}{2} = \frac{5\sqrt{5} + 3\sqrt{5} + 4\sqrt{5}}{2} = 6\sqrt{5}$

p = \frac{A B + A C + B C}{2} = \frac{5 \sqrt{5} + 3 \sqrt{5} + 4 \sqrt{5}}{2} = 6 \sqrt{5}

Do đó, bán kính đường tròn nội tiếp tam giác ABC là

$r = \sqrt{\frac{(p – a)(p – b)(p – c)}{p}} = \sqrt{\frac{(6\sqrt{5} – 5\sqrt{5})(6\sqrt{5}-3\sqrt{5})(6\sqrt{5}-4\sqrt{5})}{6\sqrt{5}}} = \sqrt{5}$

r = \sqrt{\frac{(p - a) (p - b) (p - c)}{p}} = \sqrt{\frac{(6 \sqrt{5} - 5 \sqrt{5}) (6 \sqrt{5} - 3 \sqrt{5}) (6 \sqrt{5} - 4 \sqrt{5})}{6 \sqrt{5}}} = \sqrt{5}

Dạng 3: Viết phương trình đường tròn nội tiếp tam giác ABC khi biết tọa độ 3 đỉnh

Ví dụ: Trong mặt phẳng hệ tọa độ Oxy, cho tam giác ABC có A(11; -7), B(23;9), C(-1,2). Viết phương trình đường tròn nội tiếp tam giác ABC.

Giải:

Ta có phương trình cạnh BC: 7x-24y+55=0

Phương trình đường phân giác góc A: 7x+y-70=0

Gọi D là chân đường phân giác trong đỉnh A. Tọa độ D là nghiệm của hệ:

$\left\{\begin{matrix} 7x+y-70=0\\ 7x-24y+55=0\ \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x=\frac{65}{7}\\ y=5 \end{matrix}\right. \Rightarrow D\left ( \frac{65}{7}; 5 \right )$

{\begin{matrix} 7 x + y - 70 = 0 \\ 7 x - 24 y + 55 = 0 \end{matrix} \Leftrightarrow {\begin{matrix} x = \frac{65}{7} \\ y = 5 \end{matrix} \Rightarrow D (\frac{65}{7}; 5)

Gọi I(a,b) là tâm đường tròn nội tiếp tam giác ABC.

Ta có:

$\underset{IA}{\rightarrow} = (11-a;-7-b), \underset{ID}{\rightarrow} = (\frac{65}{7}-a; 5-b), BA = 20, BD= \frac{100}{7}$

\underset{I A}{\to} = (11 - a; - 7 - b), \underset{I D}{\to} = (\frac{65}{7} - a; 5 - b), B A = 20, B D = \frac{100}{7}

$\underset{ID}{\rightarrow} = -\frac{BD}{BA}\underset{IA}{\rightarrow} \Leftrightarrow \left\{\begin{matrix} \frac{65}{7}-a = -\frac{5}{7}(11-a)\\ 5-b = -\frac{5}{7}(-7-b) \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} a=10\\ b=0 \end{matrix}\right.$

\underset{I D}{\to} = - \frac{B D}{B A} \underset{I A}{\to} \Leftrightarrow {\begin{matrix} \frac{65}{7} - a = - \frac{5}{7} (11 - a) \\ 5 - b = - \frac{5}{7} (- 7 - b) \end{matrix} \Leftrightarrow {\begin{matrix} a = 10 \\ b = 0 \end{matrix}

Vậy tọa độ I(10,0)

Bán kính đường tròn nội tiếp: r=d(I,AB)=5

(x - 10)^{2} + y^{2} = 25

Ví dụ 2: Trong tam giác ABC có AB = 3cm, AC = 7cm, BC = 8cm. Bán kính r đường tròn nội tiếp tam giác ABC bằng?

Hướng dẫn

- Chu vi tam giác ABC: p = 9.

$r = \dfrac {2\sqrt{3}} {3}$

r = \frac{2 \sqrt{3}}{3}

Ví dụ 3 $B(\dfrac {1}{4}; 0)$

B (\frac{1}{4}; 0)

6. Bài tập vận dụng đường tròn nội tiếp tam giác

Bài 1

a) Hãy vẽ một đường tròn với tâm O và bán kính 2cm.

b) Tiếp theo, vẽ một hình vuông nội tiếp trong đường tròn (O) đã vẽ ở phần a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông vừa vẽ và vẽ đường tròn (O; r).

Vẽ hình minh họa cho các bước trên.

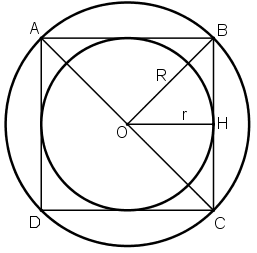
b) Vẽ hai đường kính AC và BD vuông góc với nhau. Kết nối các điểm A với B, B với C, C với D, và D với A để tạo thành hình vuông ABCD nội tiếp trong đường tròn (O; 2cm).

c) Vẽ đoạn thẳng OH vuông góc với cạnh BC.

⇒ OH là khoảng cách từ tâm O đến cạnh BC.

Do AB = BC = CD = DA (vì ABCD là hình vuông), khoảng cách từ tâm O đến các cạnh AB, BC, CD, DA đều bằng nhau (theo định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây).

⇒ O là tâm của đường tròn nội tiếp hình vuông ABCD.

OH chính là bán kính r của đường tròn nội tiếp hình vuông ABCD.

Trong tam giác vuông OBC, OH là đường trung tuyến ⇒ OH = 1/2 BC = BH.

Xét tam giác vuông OHB, ta có: r² + r² = OB² = 2² ⇒ 2r² = 4 ⇒ r² = 2 ⇒ r = √2 (cm).

Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc với bốn cạnh của hình vuông tại trung điểm của mỗi cạnh.

Bài 2

a) Hãy vẽ một tam giác đều ABC với độ dài cạnh a = 3cm.

b) Tiếp theo, vẽ đường tròn (O; R) ngoại tiếp tam giác đều ABC và tính bán kính R.

c) Sau đó, vẽ đường tròn (O; r) nội tiếp tam giác đều ABC và tính bán kính r.

d) Cuối cùng, vẽ tam giác đều IJK ngoại tiếp đường tròn (O; R).

GIẢI

Vẽ hình minh họa cho các bước trên.

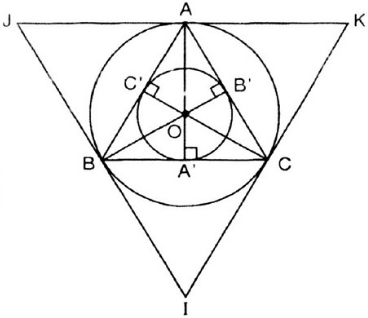
a) Sử dụng thước có chia khoảng và compa, vẽ tam giác đều ABC với cạnh dài 3cm.

+ Đầu tiên, dựng đoạn thẳng AB = 3cm.

+ Sau đó, dựng cung tròn tâm A bán kính 3cm và cung tròn tâm B bán kính 3cm. Hai cung tròn này cắt nhau tại điểm C.

Nối các điểm A với C và B với C để hoàn thành tam giác đều ABC có cạnh 3cm.

b) Gọi A', B', C' lần lượt là trung điểm của các cạnh BC, AC, và AB.

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, và ba phân giác AA', BB', CC' của tam giác đều ABC).

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực này cắt nhau tại điểm O.

Vẽ đường tròn tâm O với bán kính R = OA = OB = OC, ta thu được đường tròn ngoại tiếp tam giác ABC.

Tính độ dài AA':

GIẢI

A^{'} C = \frac{3}{2}

A C^{2} = A A^{' 2} + A^{'} C^{2} \Rightarrow A A^{' 2} = 3^{2} - \frac{3^{2}}{4} = \frac{9}{4} \Rightarrow A A^{'} = \frac{3 \sqrt{3}}{2}

$OA = \dfrac{2}{3}AA$

O A = \frac{2}{3} A A^{'}

$R = OA = \dfrac{2}{3}AA$

R = O A = \frac{2}{3} A A^{'} = \frac{2}{3} . \frac{3 \sqrt{3}}{2} = \sqrt{3}

c) Vì tam giác ABC là tam giác đều, các trung điểm A', B', C' của các cạnh BC, CA, AB đồng thời là chân đường phân giác hạ từ các đỉnh A, B, C xuống các cạnh tương ứng.

Đường tròn nội tiếp (O; r) tiếp xúc với ba cạnh của tam giác đều ABC tại các trung điểm A', B', C'.

Hay nói cách khác, đường tròn (O; r) là đường tròn có tâm O và bán kính r = OA' = OB' = OC'.

r = O A^{'} = \frac{1}{3} A A^{'} = \frac{1}{3} . \frac{3 \sqrt{3}}{2} = \frac{\sqrt{3}}{2}

d) Vẽ các tiếp tuyến với đường tròn (O; R) tại các điểm A, B, C. Ba tiếp tuyến này cắt nhau tại các điểm I, J, K, tạo thành tam giác đều IJK ngoại tiếp đường tròn (O; R).

Bài 3

$\overparen{AB}, \overparen{BC}, \overparen{CD}$

\overset{⏜}{A B}, \overset{⏜}{B C}, \overset{⏜}{C D}

$sđ\overparen{AB} = 60^0, sđ\overparen{BC} = 90^0, sđ\overparen{CD} = 120^0$

s đ \overset{⏜}{A B} = 60^{0}, s đ \overset{⏜}{B C} = 90^{0}, s đ \overset{⏜}{C D} = 120^{0}

a) Tứ giác ABCD thuộc loại hình gì?

b) Hãy chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác ABCD theo bán kính R.

GIẢI

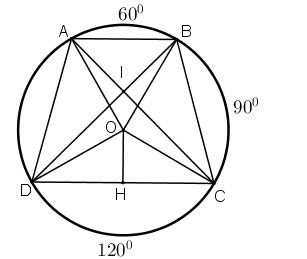
a) Xét đường tròn (O), ta có:

$\displaystyle \widehat {BA{\rm{D}}} = {{{{90}^0} + {{120}^0}} \over 2} = {105^0}$

\hat{B A D} = \frac{90^{0} + 120^{0}}{2} = 105^{0}

$\overparen{BCD})$

\overset{⏜}{B C D})

$\displaystyle \widehat {A{\rm{D}}C} = {{{{60}^0} + {{90}^0}} \over 2} = {75^0}$

\hat{A D C} = \frac{60^{0} + 90^{0}}{2} = 75^{0}

$\overparen{ABC}$

\overset{⏜}{A B C}

Từ (1) và (2), ta có:

$\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}C} = {105^0} + {75^0} = {180^0}$

\hat{B A D} + \hat{A D C} = 105^{0} + 75^{0} = 180^{0}

$\widehat {BA{\rm{D}}}$

\hat{B A D}

$\widehat {A{\rm{D}}C}$

\hat{A D C}

Đẳng thức (3) chứng tỏ AB song song với CD. Do đó, tứ giác ABCD là hình thang, và vì nó nội tiếp đường tròn nên là hình thang cân.

$sđ\overparen{BC} = sđ\overparen{AD} = 90^0)$

s đ \overset{⏜}{B C} = s đ \overset{⏜}{A D} = 90^{0})

b) Giả sử hai đường chéo AC và BD giao nhau tại điểm I.

$\widehat {CI{\rm{D}}}$

\hat{C I D}

$\displaystyle \widehat {CI{\rm{D}}} =\dfrac{sđ\overparen{AB}+sđ\overparen{CD}}{2}=\displaystyle {{{{60}^0} + {{120}^0}} \over 2} = {90^0}$

\hat{C I D} = \frac{s đ \overset{⏜}{A B} + s đ \overset{⏜}{C D}}{2} = \frac{60^{0} + 120^{0}}{2} = 90^{0}

A C ⊥ B D .

$sđ\overparen{AB}= 60^0$

s đ \overset{⏜}{A B} = 60^{0}

$\widehat {AOB} = {60^0}$

\hat{A O B} = 60^{0}

=> Tam giác AOB đều, suy ra AB = OA = OB = R.

$\overparen{BC} = {90^0} \Rightarrow \widehat {BOC} = {90^0}$

\overset{⏜}{B C} = 90^{0} \Rightarrow \hat{B O C} = 90^{0}

$\Rightarrow BC = \sqrt{OB^2+OC^2}=R\sqrt2.$

\Rightarrow B C = \sqrt{O B^{2} + O C^{2}} = R \sqrt{2} .

O H ⊥ C D .

$\Rightarrow \widehat{BCD}=\widehat{ADC}=75^0.$

\Rightarrow \hat{B C D} = \hat{A D C} = 75^{0} .

$\Delta BOC$

Δ B O C

$\Rightarrow \widehat{BCO}=45^0.$

\Rightarrow \hat{B C O} = 45^{0} .

$\Rightarrow \widehat{OCD}=\widehat{BCD}-\widehat{BCO}=75^0-45^0=30^0.$

\Rightarrow \hat{O C D} = \hat{B C D} - \hat{B C O} = 75^{0} - 45^{0} = 30^{0} .

$\Delta OCH$

Δ O C H

$HC=OC.\cos \widehat{OCH}=\dfrac{R\sqrt{3}}{2}.$

H C = O C . \cos \hat{O C H} = \frac{R \sqrt{3}}{2} .

Điểm H là trung điểm của đoạn CD, theo định lý đường kính vuông góc với dây cung sẽ đi qua trung điểm của dây đó.

Từ đó suy ra, độ dài CD được tính bằng công thức: CD = 2.CH = R√3.

\Rightarrow C D = 2. C H = R \sqrt{3} .

Bài 4

Hãy vẽ hình lục giác đều, hình vuông và tam giác đều nội tiếp trong đường tròn (O; R), sau đó tính độ dài cạnh của các hình này theo bán kính R.

GIẢI

Các bước vẽ hình:

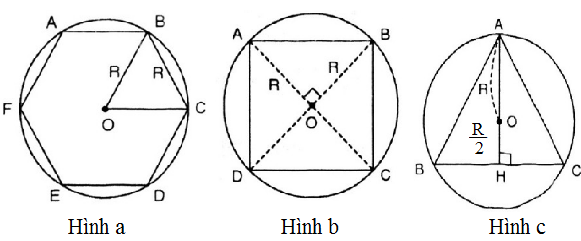
+) Hình a.

$Các cung tròn được ký hiệu lần lượt là: \overparen{{A_1}{A_2}}, \overparen{{A_2}{A_3}},...,\overparen{{A_6}{A_1}}.$

\overset{⏜}{A_{1} A_{2}}, \overset{⏜}{A_{2} A_{3}}, . . ., \overset{⏜}{A_{6} A_{1}}

${A_1}$

A_{1}

${A_2}, {A_2}$

A_{2}, A_{2}

${A_3},…, {A_6}$

A_{3}, \dots, A_{6}

₁ ${A_1}{A_2}{A_3}{A_4}{A_5}{A_6}$

A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}

Tính toán bán kính:

${a_i}$

a_{i}

${a_6}= R (vì O{A_1}{A_2}$

a_{6} = R (v ì O A_{1} A_{2}

+) Hình b.

Hướng dẫn cách vẽ:

A_{1} A_{3}

A_{2} A_{4} ⊥ A_{1} A_{3}

A_{1} A_{2} A_{3} A_{4}

A_{1}

A_{2}; A_{2}

A_{3}; A_{3}

₄₁

A_{1} A_{2} A_{3} A_{4}

Tính toán bán kính:

Gọi độ dài cạnh của hình vuông là a.

$O{A_1}{A_2}$

O A_{1} A_{2}

${a^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow a = R\sqrt 2$

a^{2} = R^{2} + R^{2} = 2 R^{2} \Rightarrow a = R \sqrt{2}

+) Hình c:

Cách vẽ tương tự như câu a) hình a.

${A_1}{A_3}{A_5}$

A_{1} A_{3} A_{5}

Tính toán bán kính:

Gọi độ dài cạnh của tam giác đều là a.

${A_1}H =A_1O+OH= R+\dfrac{R}{2} = \dfrac{3R}{2}$

A_{1} H = A_{1} O + O H = R + \frac{R}{2} = \frac{3 R}{2}

${A_3}H = \dfrac{AA$

A_{3} H = \frac{A A^{'}}{2} = \frac{a}{2}

${A_1}{A_3}=a$

A_{1} A_{3} = a

${A_1}H{A_3}$

A_{1} H A_{3}

${A_1}{H^2} = {A_1}{A_3}^2 - {A_3}{H^2}.$

A_{1} H^{2} = A_{1} {A_{3}}^{2} - A_{3} H^{2} .

$\dfrac{9R^{2}}{4} = a^2 - \dfrac{a^{2}}{4}.$

\frac{9 R^{2}}{4} = a^{2} - \frac{a^{2}}{4} .

$\Rightarrow{a^2} = 3{R^2} \Rightarrow a = R\sqrt 3$

\Rightarrow a^{2} = 3 R^{2} \Rightarrow a = R \sqrt{3}

Bài tập 5: Cho tam giác MNP biết MN = 8cm, MP = 9cm, NP = 11cm. Hỏi bán kính đường tròn nội tiếp tam giác MNP bằng bao nhiêu?

Giải

Nửa chu vi tam giác MNP là:

$p=\frac{a+b+c}{2}=\frac{8+9+11}{2}=14$

p = \frac{a + b + c}{2} = \frac{8 + 9 + 11}{2} = 14

Theo công thức Heron, diện tích tam giác MNP là:

$S=\sqrt{p(p-M N)(p-M P)(p-N P)}$

S = \sqrt{p (p - M N) (p - M P) (p - N P)}

$\begin{aligned} &=\sqrt{14(14-8)(14-9)(14-11)} \\ &=6 \sqrt{35} \end{aligned}$

\begin{matrix} = \sqrt{14 (14 - 8) (14 - 9) (14 - 11)} \\ = 6 \sqrt{35} \end{matrix}

Bán kính đường tròn nội tiếp tam giác MNP được tính bằng công thức:

$r=\frac{S}{p}=\frac{6 \sqrt{35}}{14}$

r = \frac{S}{p} = \frac{6 \sqrt{35}}{14}

Bài 5:

Cho tam giác MNP đều với độ dài cạnh là 2a. Hãy tính bán kính đường tròn nội tiếp của tam giác này.

Lời giải chi tiết:

Diện tích của tam giác đều MNP được xác định bởi công thức:

S = ½ MN.MP.sinM

= ½ .2a.2a.sin60^o

= a²√3

Nửa chu vi của tam giác MNP được tính như sau:

$p=\frac{2 a+2 a+2 a}{2}=3 a$

p = \frac{2 a + 2 a + 2 a}{2} = 3 a

$r=\frac{S}{p}=\frac{a^{2} \sqrt{3}}{3 a}=\frac{a \sqrt{3}}{3}=\frac{a}{\sqrt{3}}$

r = \frac{S}{p} = \frac{a^{2} \sqrt{3}}{3 a} = \frac{a \sqrt{3}}{3} = \frac{a}{\sqrt{3}}

Bài 6

Cho tam giác ABC biết AB = 12cm, AC = 13cm, BC = 15cm. Tính bán kính đường tròn nội tiếp tam giác ABC

Lời giải

Nửa chu vi của tam giác ABC được tính như sau:

$p=\frac{A B+A C+B C}{2}=\frac{12+13+15}{2}=20$

p = \frac{A B + A C + B C}{2} = \frac{12 + 13 + 15}{2} = 20

$S=\sqrt{20(20-12)(20-13)(20-15)}=20 \sqrt{14}$

S = \sqrt{20 (20 - 12) (20 - 13) (20 - 15)} = 20 \sqrt{14}

$r=\frac{S}{p}=\frac{20 \sqrt{14}}{20}=\sqrt{14}$

r = \frac{S}{p} = \frac{20 \sqrt{14}}{20} = \sqrt{14}

Bài 7

Cho △ABC với đường tròn (I) tiếp xúc với các cạnh AB, AC lần lượt tại D và E. Chứng minh nếu AB < AC thì BE < CD.

Giải

Hãy vẽ một hình minh họa để dễ dàng quan sát và phân tích bài toán.

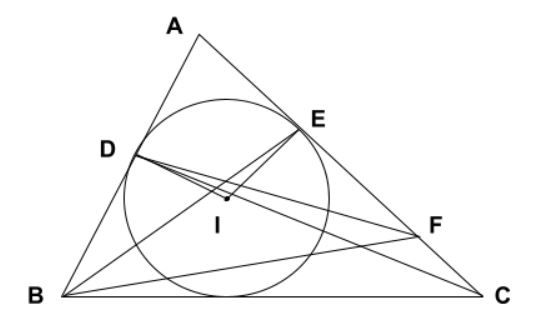
Do AB < AC, ta lấy điểm F trên cạnh AC sao cho AB = AF.

Từ đó, △ABF trở thành tam giác cân tại A. Vì AD = AE, suy ra BD = FE, dẫn đến tứ giác BDEF là hình thang cân.

Do đó, BE = FD.

Xét △ABF cân tại A, góc ∠AFB là góc ở đáy nên là góc nhọn.

Từ đó, ∠AFD cũng là góc nhọn, suy ra ∠DFC là góc tù.

Vậy nên, CD > FD = BE (điều phải chứng minh).

7. Bài tập tự luyện tâm đường tròn nội tiếp tam giác

Bài tập 1. Trong mặt phẳng Oxy, cho tam giác ABC với các tọa độ A(1;5), B(–4;–5) và C(4;-1). Hãy xác định tọa độ tâm J của đường tròn nội tiếp tam giác ABC.

Đáp số: J(1;0)

Bài tập 2. Trong mặt phẳng Oxy, cho tam giác ABC với các tọa độ A(-15/2; 2), B(12; 15) và C(0; -3). Tìm tọa độ tâm J của đường tròn nội tiếp tam giác ABC.

Đáp số: J(-1;2)

Bài tập 3. Trong mặt phẳng Oxy, cho tam giác ABC với các tọa độ A(3;–1), B(1;5) và C(6;0). Gọi A’ là chân đường cao kẻ từ đỉnh A xuống cạnh BC. Hãy tìm tọa độ của A’.

Đáp số: A’(5;1)

Bài tập 4: Cho tam giác MNP cân tại M, ngoại tiếp đường tròn có bán kính 3 cm. Gọi H và K lần lượt là giao điểm của đường tròn nội tiếp tam giác MNP với hai cạnh MN và NP. Biết MH = 4 cm. Hãy tính diện tích của tam giác cân MNP.

Bài tập 5

Cho tam giác đều MNP. Gọi O là giao điểm của hai đường phân giác hai góc trong của tam giác đều MNP, và H là chân đường vuông góc kẻ từ điểm O đến cạnh NP. Biết rằng đường tròn nội tiếp tam giác đều MNP có bán kính bằng 2 cm. Hãy tính độ dài các cạnh của tam giác đều MNP.

Bài tập 6

Cho tam giác MNP. Gọi (O) là đường tròn nội tiếp tam giác MNP. Biết rằng (O) tiếp xúc với hai cạnh MN và MP lần lượt tại hai điểm H và K. Biết MH . MP = MK . MN. Chứng minh rằng tam giác MNP là tam giác cân tại M.

Bài tập 7

Cho tam giác MNP. Gọi O là giao điểm của ba đường phân giác các góc trong của tam giác MNP. Gọi H, K, L lần lượt là chân các đường vuông góc kẻ từ điểm O đến các cạnh NP, MN, MP. Chứng minh rằng: