Hai Đường Thẳng Song Song: Lý Thuyết Cơ Bản và Phương Pháp Chứng Minh Qua Bài Tập

Hai đường thẳng song song: Định nghĩa và phương pháp chứng minh Tính chất của hai đường thẳng song song là gì? Đây là câu hỏi mà rất nhiều học sinh đặt ra khi tìm hiểu về chủ đề này.

Hai đường thẳng song song là một chủ đề không thể thiếu trong chương trình toán học phổ thông, được giảng dạy từ lớp 6 đến lớp 11 và có nhiều ứng dụng thực tiễn. Trong bài viết này, EduTOPS sẽ cung cấp cho bạn toàn bộ kiến thức về hai đường thẳng song song, bao gồm dấu hiệu nhận biết, tính chất, phương pháp chứng minh, và các bài tập vận dụng. Thông qua tài liệu này, bạn sẽ có thêm nguồn tham khảo hữu ích để củng cố kiến thức và giải quyết các bài toán một cách hiệu quả.

1. Khái niệm hai đường thẳng song song

Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không bao giờ giao nhau, không có điểm chung nào.

2. Các dấu hiệu nhận biết hai đường thẳng song song

Dấu hiệu 1: Dựa trên định nghĩa cơ bản của hai đường thẳng song song.

Dấu hiệu 2: Dựa vào việc xét một đường thẳng cắt hai đường thẳng cần kiểm tra.

Nếu một đường thẳng c cắt hai đường thẳng a và b, đồng thời tạo thành một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau, thì a và b song song với nhau.

Dấu hiệu 3: Dựa vào mối quan hệ từ vuông góc đến song song.

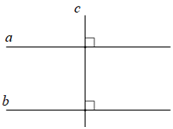
Nếu đường thẳng a vuông góc với đường thẳng c và đường thẳng b cũng vuông góc với đường thẳng c (với a và b là hai đường thẳng phân biệt), thì a song song với b (xem hình minh họa).

Ta có công thức sau:

Dấu hiệu 4: Dựa vào tính chất cùng song song với một đường thẳng thứ ba.

Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba, thì chúng song song với nhau.

3. Tính chất của hai đường thẳng song song

Khi một đường thẳng cắt hai đường thẳng song song, các tính chất sau đây được áp dụng:

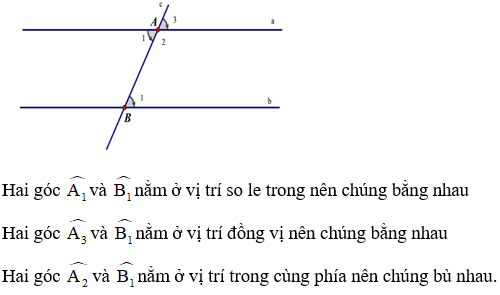
- Các góc so le trong bằng nhau.

- Các góc đồng vị bằng nhau.

- Các góc trong cùng phía bù nhau.

Xét đường thẳng c cắt hai đường thẳng song song a và b như trong hình minh họa:

4. Phương pháp vẽ hai đường thẳng song song

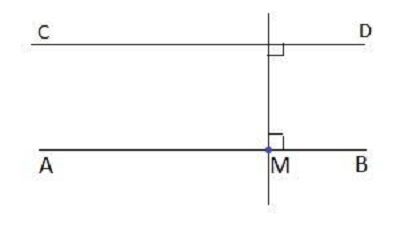
Để vẽ đường thẳng CD đi qua điểm E và song song với đường thẳng AB cho trước, ta thực hiện các bước sau:

Cách thực hiện như sau:

Bước 1: Vẽ đường thẳng MN đi qua điểm E và vuông góc với đường thẳng AB.

Bước 2: Vẽ đường thẳng CD đi qua điểm E và vuông góc với đường thẳng MN. Khi đó, đường thẳng CD sẽ song song với đường thẳng AB.

5. Các phương pháp chứng minh hai đường thẳng song song

- Phương pháp 1: Xác định hai góc trong cùng phía có tổng bằng 180 độ (bù nhau).

- Phương pháp 2: Chứng minh hai góc so le trong bằng nhau.

- Phương pháp 3: Chứng minh các góc đồng vị bằng nhau.

- Phương pháp 4: Áp dụng tiên đề Ơ-clít: "Qua một điểm nằm ngoài đường thẳng, chỉ có duy nhất một đường thẳng song song với đường thẳng đã cho."

- Phương pháp 5: Chứng minh hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.

- Phương pháp 6: Chứng minh hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.

6. Bài tập áp dụng về hai đường thẳng song song

Bài tập 1: Cho tam giác ABC, với M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm D sao cho MA = MD. Hãy chứng minh rằng AB song song với CD.

Bài tập 2: Cho tam giác ABC, M và N lần lượt là trung điểm của AB và AC. Trên tia đối của tia MC, lấy điểm D sao cho MD = MC. Trên tia đối của tia NB, lấy điểm E sao cho NE = NB. Chứng minh rằng DE song song với BC.

Bài tập 3: Cho tam giác cân ABC với AB = AC. Trên các cạnh AB và AC, lấy lần lượt các điểm D và E sao cho AD = AE. Hãy chứng minh rằng DE song song với BC.