Mới nhất Ngữ văn IELTS TOEIC Từ vựng tiếng Anh Tiếng Anh giao tiếp Tiếng Anh THPT Kỹ năng tiếng Anh Ngôn ngữ khác

Nội dung bài viết

I. Tóm tắt lý thuyết lũy thừa số hữu tỉ
II. Bài tập lũy thừa lớp 7 (Tự luyện)
III. Các dạng bài tập về lũy thừa lớp 7 có đáp án

Chuyên đề Lũy thừa của số hữu tỉ: Tổng hợp các dạng bài tập Toán lớp 7 chi tiết và đầy đủ

Chia sẻ

Bài tập lũy thừa lớp 7 là tài liệu tổng hợp lý thuyết và các dạng bài tập đa dạng, kèm đáp án chi tiết và bài tự luyện. Thông qua đó, học sinh có thể củng cố và mở rộng kiến thức, nâng cao kỹ năng giải toán về lũy thừa một cách hiệu quả.

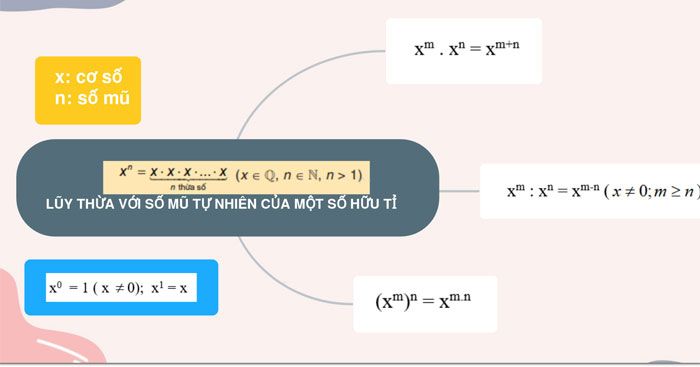
Các dạng bài tập về lũy thừa lớp 7

Tài liệu về các dạng bài tập lũy thừa lớp 7 là nguồn tham khảo quý giá, giúp học sinh thử sức với nhiều dạng bài tự luận từ cơ bản đến nâng cao. Qua đó, các em không chỉ tự kiểm tra kiến thức mà còn nắm vững những gì đã học trong chương trình Toán 7. Những bài tập tự luyện được thiết kế nhằm giúp học sinh rèn luyện kỹ năng vận dụng kiến thức vào thực hành một cách thuần thục. Dưới đây là tổng hợp các dạng bài tập lũy thừa lớp 7, mời các em cùng khám phá và thực hành.

I. Tóm tắt lý thuyết lũy thừa số hữu tỉ

1. Luỹ thừa với số mũ tự nhiên.

Luỹ thừa bậc n của một số hữu tỉ, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1): xⁿ= x.x.x.x.x.x

Quy ước: x¹ = x; x⁰ = 1; (x ¹ 0)

$\frac{a}{b}(a, b \in Z, b \neq 0)$ $\left(\frac{a}{b}\right)^{n}=\frac{a^{n}}{b^{n}}$

2.Tích và thương của hai luỹ thừa cùng cơ số:

$x^{m} \cdot x^{n}=x^{m+n} \quad x^{m}: x^{n}=x^{m-n}(\mathrm{x} \neq 0, m \geq n)$

a) Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

b) Khi chia hai luỹ thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của luỹ thừa bị chia trừ đi số mũ của luỹ thừa chia.

3. Luỹ thừa của luỹ thừa. $\left(x^{m}\right)^{n}=x^{m \cdot n}$ 4. Luỹ thừa của một tích - luỹ thừa của một thương $(x \cdot y)^{n}=x^{n} \cdot y^{n} \quad(x: y)^{n}=x^{n}: y^{n}(\mathrm{y} \neq 0)$ 5. Tóm tắt các công thức về lũy thừa $\mathrm{x}, \mathrm{y} \in \mathrm{Q} ; \mathrm{x}=\frac{a}{b} \mathrm{y}=\frac{c}{d}$ $\left(\frac{a}{b}\right)^{\mathrm{m}} \cdot\left(\frac{a}{b}\right)^{\mathrm{n}}=\left(\frac{a}{b}\right)^{\mathrm{m}+\mathrm{n}}$ $\left(\frac{a}{b}\right)^{\mathrm{m}}:\left(\frac{a}{b}\right)^{\mathrm{n}}=\left(\frac{a}{b}\right)^{\mathrm{m}-\mathrm{n}}(\mathrm{m} \geq \mathrm{n})$ $(\mathrm{x} \cdot \mathrm{y})^{\mathrm{m}}=\mathrm{x}^{\mathrm{m}} \cdot \mathrm{y}_{\mathrm{m}}^{\mathrm{m}}$ $(\mathrm{x}: \mathrm{y})^{\mathrm{m}}=\mathrm{x}_{m}^{\mathrm{m}}: \mathrm{y}_{m}^{\mathrm{m}}$ $\left(\mathrm{x}^{\mathrm{m}}\right)^{\mathrm{n}}=\mathrm{x}_{\mathrm{m}}^{\mathrm{m} \cdot \mathrm{n}}$ $\mathrm{x}^{\mathrm{n}}=\frac{1}{x^{-n}}$ $\mathrm{a}^{1}=\mathrm{a} ; \mathrm{a}^{0}=1.$

- Giá trị tuyệt đối

$+ ) Với x \in Q thì |x|=\left\{\begin{array}{c}x \text { nếu } x \geq 0 \\ -x \text { nếu } x<0\end{array}\right.$

II. Bài tập lũy thừa lớp 7 (Tự luyện)

Bài 1: Tính giá trị của:

M = 100²– 99² + 98² – 97² + … + 2² – 1²;

N = (20²+ 18² + 16² + … + 4² + 2²) – (19² + 17² + 15² + … + 3² + 1²);

P = (-1)ⁿ.(-1)²ⁿ⁺¹.(-1)ⁿ⁺¹.

Bài 2: Tìm x biết rằng:

a) (x – 1)³ = 27;

b) x² + x = 0;

c) (2x + 1)² = 25;

d) (2x – 3)² = 36;

e) 5^{x + 2} = 625;

f) (x – 1)^{x + 2} = (x – 1)^{x + 4};

g) (2x – 1)³ = -8.

h) = 2x;

Bài 3: Tìm số nguyên dương n biết rằng:

a) 32 < 2ⁿ<128;

b) 2.16 ≥ 2ⁿ > 4;

c) 9.27 ≤ 3ⁿ ≤ 243.

Bài 4: So sánh:

a) 99²⁰và 9999¹⁰;

b) 3²¹và 2³¹;

c) 2³⁰ + 3³⁰ + 4³⁰ và 3.24¹⁰.

Bài 5: Chứng minh rằng nếu a = x³y; b = x²y²; c = xy³ thì với bất kì số hữu tỉ x và y nào ta cũng có: ax + b² – 2x⁴y⁴ = 0 ?

Bài 6: Chứng minh đẳng thức: 1 + 2 + 2² + 2³ + … + 2⁹⁹ + 2¹⁰⁰ = 2¹⁰¹ – 1.

Bài 7: Tính

$a) \left(-\frac{1}{3}\right)^{2} \cdot\left(-\frac{1}{3}\right)$ $b) (-2)^{2} \cdot(-2)^{3}$ $c) a^{5} \cdot a^{7}$

Bài 8: Tính

$a) \left(2^{2}\right)^{\left(2^{2}\right)}$ $b) \frac{8^{14}}{4^{12}}$ $c) \frac{\left(-\frac{5}{7}\right)^{n+1}}{\left(-\frac{5}{7}\right)^{n}}(n \geq 1)$

Bài 9: Tìm x, biết:

$a) \left(-\frac{2}{3}\right)^{2} \cdot x=\left(-\frac{2}{3}\right)^{5}$ $b) \left(-\frac{1}{3}\right)^{3} \cdot x=\frac{1}{81}$

Bài 10: Tính

$a) \left(-\frac{1}{3}\right)^{7} \cdot 3^{7}$ $b) (0,125)^{3} .512$ $c) \frac{90^{2}}{15^{2}}$ $d) \frac{790^{4}}{79^{4}}$ Bài 11: $2^{24}$ $3^{16}$

Bài 12: Tính giá trị biểu thức

$a) \frac{45^{10} .5^{10}}{75^{10}}$ $b) \frac{(0,8)^{5}}{(0,4)^{6}}$ $c) \frac{2^{15} \cdot 9^{4}}{6^{3} \cdot 8^{3}}$ $d) \frac{8^{10}+4^{10}}{8^{4}+4^{11}}$

Bài 13: Tính

$a. \left(\frac{1}{5}\right)^{5} \cdot 5^{5}$ $b. \left(\frac{1}{5}\right)^{3} \cdot 10^{3}$ $c. \left(-\frac{2}{3}\right)^{4}: 2^{4}$ $d. \left(\frac{2}{3}\right)^{4} \cdot 9^{2}$ $e. \left(\frac{1}{2}\right)^{3} \cdot\left(\frac{1}{4}\right)^{2}$ $f. \frac{120^{3}}{40^{3}}$ $g. \frac{390^{4}}{130^{4}}$ $h.16/ (0,125)^{3} \cdot 512;$

Bài 14: Dùng 10 chữ số khác nhau để biểu diễn số 1 mà không dùng các phép tính cộng, trừ,
nhân, chia.

Bài 15: Tính:

$a) (0,25)^{3} .32$ $b) (-0,125)^{3} \cdot 80^{4};$ $c) \frac{8^{2} \cdot 4^{5}}{2^{20}}$ $d) \frac{81^{11} \cdot 3^{17}}{27^{10} \cdot 9^{15}}.$ Bài 16: $\mathrm{x} \in \mathrm{Q}$ $\mathrm{x} \neq 0$ $\mathrm{x}^{12}$ $\mathrm{x}^{9}$ $x^{4}$ $\mathrm{x}^{15}$

Bài 17: Tính nhanh:

$a) \mathrm{A}=2008^{(1.9 .4 .6)(\cdot(9.4 .7) \ldots(1.99 .9)};$ $b) \mathrm{B}=\left(1000-1^{3}\right) \cdot\left(1000-2^{3}\right) \cdot\left(1000-3^{3}\right) \ldots\left(1000-50^{3}\right).$

III. Các dạng bài tập về lũy thừa lớp 7 có đáp án

Bài 1

Viết các số sau dưới dạng lũy thừa với số mũ lớn hơn 1:

$0,49;\frac{1}{{32}};\frac{{ - 8}}{{125}};\frac{{16}}{{81}};\frac{{121}}{{169}}$

Gợi ý đáp án:

Thực hiện các phép tính như sau:

$0,49 = 0,7.0,7 = {\left( {0,7} \right)^2}$ $\frac{1}{{32}} = \frac{1}{{2.2.2.2.2}} = \frac{1}{{{2^5}}} = \frac{{{1^5}}}{{{2^5}}} = {\left( {\frac{1}{2}} \right)^5}$ $\frac{{ - 8}}{{125}} = \frac{{\left( { - 2} \right).\left( { - 2} \right).\left( { - 2} \right)}}{{5.5.5}} = \frac{{{{\left( { - 2} \right)}^3}}}{{{5^3}}} = {\left( {\frac{{ - 2}}{5}} \right)^3}$ $\frac{{16}}{{81}} = \frac{{4.4}}{{9.9}} = \frac{{{4^2}}}{{{9^2}}} = {\left( {\frac{4}{9}} \right)^2}$ $\frac{{121}}{{169}} = \frac{{11.11}}{{13.13}} = \frac{{{{11}^2}}}{{{{13}^2}}} = {\left( {\frac{{11}}{{13}}} \right)^2}$

Bài 2

${\left( {\frac{{ - 1}}{2}} \right)^5};{\left( {\frac{{ - 2}}{3}} \right)^4};{\left( { - 2\frac{1}{4}} \right)^3};{\left( {0,3} \right)^5};{\left( { - 25,7} \right)^0}$ ${\left( { - \frac{1}{3}} \right)^2};{\left( { - \frac{1}{3}} \right)^3};{\left( { - \frac{1}{3}} \right)^4};{\left( { - \frac{1}{3}} \right)^5}$

Hãy rút ra nhận xét về dấu của lũy thừa với số mũ chẵn và lũy thừa với số mũ lẻ của một số hữu tỉ âm.

Gợi ý đáp án:

a) Hãy thực hiện các phép tính sau đây:

$\begin{matrix} {\left( {\dfrac{{ - 1}}{2}} \right)^5} = \left( {\dfrac{{ - 1}}{2}} \right).\left( {\dfrac{{ - 1}}{2}} \right).\left( {\dfrac{{ - 1}}{2}} \right).\left( {\dfrac{{ - 1}}{2}} \right).\left( {\dfrac{{ - 1}}{2}} \right) = \dfrac{{ - 1}}{{32}} \hfill \\ {\left( { - 2\dfrac{1}{4}} \right)^3} = {\left( { - \dfrac{9}{4}} \right)^3} = \left( { - \dfrac{9}{4}} \right).\left( { - \dfrac{9}{4}} \right).\left( { - \dfrac{9}{4}} \right) = \dfrac{{ - 729}}{{64}} \hfill \\ {\left( { - 0,3} \right)^5} = \left( { - 0,3} \right).\left( { - 0,3} \right).\left( { - 0,3} \right).\left( { - 0,3} \right).\left( { - 0,3} \right) = - 0,00243 \hfill \\ {\left( { - 25,7} \right)^0} = 1 \hfill \\ \end{matrix}$

b) Tiếp tục với các phép tính sau:

$\begin{matrix} {\left( { - \dfrac{1}{3}} \right)^2} = \left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right) = \dfrac{1}{9} \hfill \\ {\left( { - \dfrac{1}{3}} \right)^3} = \left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right) = \dfrac{{ - 1}}{{27}} \hfill \\ {\left( { - \dfrac{1}{3}} \right)^4} = \left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right) = \dfrac{1}{{81}} \hfill \\ {\left( { - \dfrac{1}{3}} \right)^5} = \left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right).\left( { - \dfrac{1}{3}} \right).\left( { - \frac{1}{3}} \right) = \dfrac{{ - 1}}{{243}} \hfill \\ \end{matrix}$

Đối với số hữu tỉ âm, khi lũy thừa có số mũ chẵn, kết quả sẽ là một số hữu tỉ dương. Ngược lại, khi số mũ lẻ, kết quả sẽ là một số hữu tỉ âm.

Bài 3

Tìm giá trị của x trong các phương trình sau:

$x:{\left( {\frac{{ - 1}}{2}} \right)^3} = - \frac{1}{2}$ ${\left( {\frac{{ - 2}}{3}} \right)^{11}}:x = {\left( {\frac{{ - 2}}{3}} \right)^9}$ $x.{\left( {\frac{3}{5}} \right)^7} = {\left( {\frac{3}{5}} \right)^9}$ $x.{\left( {0,25} \right)^6} = {\left( {\frac{1}{4}} \right)^8}$

Gợi ý đáp án:

Hãy thực hiện các phép tính sau để tìm x:

$x:{\left( {\frac{{ - 1}}{2}} \right)^3} = - \frac{1}{2}$ $\begin{matrix} x = \left( { - \dfrac{1}{2}} \right).{\left( {\dfrac{{ - 1}}{2}} \right)^3} \hfill \\ x = {\left( {\dfrac{{ - 1}}{2}} \right)^1}.{\left( {\dfrac{{ - 1}}{2}} \right)^3} \hfill \\ x = {\left( {\dfrac{{ - 1}}{2}} \right)^{1 + 3}} = {\left( {\dfrac{{ - 1}}{2}} \right)^4} \hfill \\ x = \dfrac{1}{{16}} \hfill \\ \end{matrix}$ $x = \frac{1}{{16}}$ $x.{\left( {\frac{3}{5}} \right)^7} = {\left( {\frac{3}{5}} \right)^9}$ $\begin{matrix} x = {\left( {\dfrac{3}{5}} \right)^9}:{\left( {\dfrac{3}{5}} \right)^7} \hfill \\ x = {\left( {\dfrac{3}{5}} \right)^{9 - 7}} \hfill \\ x = {\left( {\dfrac{3}{5}} \right)^2} \hfill \\ x = \dfrac{9}{{25}} \hfill \\ \end{matrix}$ $x = \dfrac{9}{{25}}$ ${\left( {\frac{{ - 2}}{3}} \right)^{11}}:x = {\left( {\frac{{ - 2}}{3}} \right)^9}$ $\begin{matrix} x = {\left( {\dfrac{{ - 2}}{3}} \right)^{11}}:{\left( {\dfrac{{ - 2}}{3}} \right)^9} \hfill \\ x = {\left( {\dfrac{{ - 2}}{3}} \right)^{11 - 9}} \hfill \\ x = {\left( {\dfrac{{ - 2}}{3}} \right)^2} \hfill \\ x = \dfrac{4}{9} \hfill \\ \end{matrix}$ $x = \dfrac{4}{9}$ $x.{\left( {0,25} \right)^6} = {\left( {\frac{1}{4}} \right)^8}$ $\begin{matrix} x = {\left( {\dfrac{1}{4}} \right)^8}:{\left( {0,25} \right)^6} \hfill \\ x = {\left( {\dfrac{1}{4}} \right)^8}:{\left( {\dfrac{1}{4}} \right)^6} \hfill \\ x = {\left( {\dfrac{1}{4}} \right)^{8 - 6}} = {\left( {\dfrac{1}{4}} \right)^2} \hfill \\ x = \dfrac{1}{{16}} \hfill \\ \end{matrix}$ $x = \frac{1}{{16}}$

Bài 4: Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ:

${25^4}{.2^8}$ $4.32:\left( {{2^3}.\frac{1}{{16}}} \right)$ ${27^2}:{25^3}$ ${8^2}:{9^3}$

Gợi ý đáp án

Hãy thực hiện các phép tính dưới đây:

${25^4}{.2^8} = {\left( {{5^2}} \right)^4}{.2^8} = {5^{2.4}}{.2^8} = {5^8}{.2^8} = {\left( {5.2} \right)^8} = {10^8}$ $4.32:\left( {{2^3}.\frac{1}{{16}}} \right) = {2^2}{.2^5}:\left( {{2^3}.\frac{1}{{{2^4}}}} \right) = {2^{2 + 5}}:\frac{1}{2} = {2^7}:\frac{1}{2} = {2^7}.2 = {2^{7 + 1}} = {2^8}$ ${27^2}:{25^3} = {\left( {{3^3}} \right)^2}:{\left( {{5^2}} \right)^3} = {3^6}:{5^6} = {\left( {\frac{3}{5}} \right)^6}$ ${8^2}:{9^3} = {\left( {{2^3}} \right)^2}:{\left( {{3^2}} \right)^3} = {2^6}:{3^6} = {\left( {\frac{2}{3}} \right)^6}$

Bài 5: Tính toán các biểu thức sau:

${4^5}:{4^2} = {4^{5 - 2}} = {4^3};{\left( { - 1\frac{1}{2}} \right)^6}:{\left( { - 1\frac{1}{2}} \right)^2} = {\left( { - 1\frac{1}{2}} \right)^{6 - 2}} = {\left( { - 1\frac{1}{2}} \right)^4}$

Bài 6: Tính giá trị các biểu thức lũy thừa sau:

Hãy phân tích và rút ra nhận xét về dấu của lũy thừa khi số mũ là chẵn hoặc lẻ đối với một số hữu tỉ âm.

Gợi ý đáp án

a) Thực hiện các phép tính như sau:

b) Hãy thực hiện các phép tính dưới đây:

Đối với số hữu tỉ âm, nếu số mũ là chẵn, kết quả sẽ là số hữu tỉ dương; nếu số mũ là lẻ, kết quả sẽ là số hữu tỉ âm.

Bài 7 Tìm giá trị của x trong các phương trình sau:

$x:{\left( {\frac{{ - 1}}{2}} \right)^3} = - \frac{1}{2}$ $x.{\left( {\frac{3}{5}} \right)^7} = {\left( {\frac{3}{5}} \right)^9}$ ${\left( {\frac{{ - 2}}{3}} \right)^{11}}:x = {\left( {\frac{{ - 2}}{3}} \right)^9}$ $x.{\left( {0,25} \right)^6} = {\left( {\frac{1}{4}} \right)^8}$