Mới nhất Ngữ văn IELTS TOEIC Từ vựng tiếng Anh Tiếng Anh giao tiếp Tiếng Anh THPT Kỹ năng tiếng Anh Ngôn ngữ khác

Nội dung bài viết

1. Định nghĩa Trọng tâm tam giác
2. Tính chất trọng tâm tam giác
3. Cách xác định trọng tâm tam giác
4. Trọng tâm của các hình học đặc biệt
5. Bài tập trọng tâm của tam giác

Trọng tâm tam giác: Khám phá khái niệm, đặc tính và phương pháp xác định chính xác

Chia sẻ

Trọng tâm tam giác là một khái niệm toán học quan trọng được giảng dạy từ lớp 7. Vậy trọng tâm là gì? Làm thế nào để xác định trọng tâm của một tam giác? Hãy cùng EduTOPS khám phá chi tiết trong bài viết dưới đây.

Trong bài học này, chúng tôi sẽ cung cấp toàn bộ kiến thức về trọng tâm tam giác, bao gồm tính chất và cách xác định, kèm theo các bài tập minh họa có lời giải chi tiết. Hy vọng tài liệu này sẽ giúp các em học sinh củng cố kiến thức và nâng cao kỹ năng giải toán, từ đó đạt kết quả tốt trong các bài kiểm tra và kỳ thi sắp tới. Ngoài ra, các em có thể tham khảo thêm về các trường hợp bằng nhau của hai tam giác.

1. Định nghĩa Trọng tâm tam giác

Trọng tâm của tam giác chính là điểm giao nhau của ba đường trung tuyến trong tam giác đó.

Theo chương trình sách giáo khoa hiện hành, học sinh lớp 7 đã được làm quen với khái niệm trọng tâm. Định nghĩa về trọng tâm được trình bày như sau: “Trong một tam giác, ba đường trung tuyến luôn gặp nhau tại một điểm duy nhất, điểm này được gọi là trọng tâm của tam giác.”

Ví dụ: Xét tam giác ABC với ba đường trung tuyến AM, BN, CP. Ba đường trung tuyến này đồng quy tại điểm G, và G chính là trọng tâm của tam giác ABC.

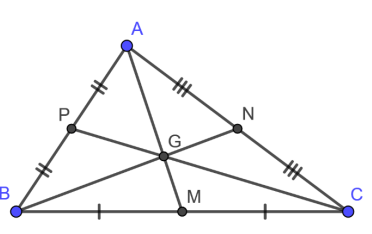
Trong tam giác ABC, các đường trung tuyến AM, BN, CP đều đi qua điểm G.

Điểm G được gọi là trọng tâm của tam giác ABC.

2. Tính chất trọng tâm tam giác

Một trong những tính chất quan trọng của trọng tâm tam giác là khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến tương ứng với đỉnh đó.

Giả sử tam giác ABC có ba đường trung tuyến AM, BN, CP và G là trọng tâm. Theo tính chất này, ta có các tỉ lệ sau:

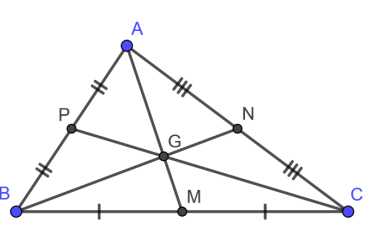
Tam giác ABC với G là trọng tâm

Khi đó, các tỉ lệ được biểu diễn như sau:

G A = \frac{2}{3} A M; G B = \frac{2}{3} B N; G C = \frac{2}{3} C P

Ví dụ: Cho tam giác ABC có trọng tâm G. Biết AM là đường trung tuyến với M thuộc cạnh BC và AM = 12cm. Hãy tính độ dài đoạn AG và GM.

Ngoài ra, còn có một số hằng đẳng thức khác liên quan đến trọng tâm tam giác. Xét từ góc độ này, điểm G chia mỗi đường trung tuyến thành ba phần bằng nhau.

- Đối với đường trung tuyến AM, ta có:

\frac{3}{2}

\frac{1}{2}

- Đối với đường trung tuyến BN, ta có:

\frac{3}{2}

\frac{1}{2}

- Đối với đường trung tuyến CP, ta có:

\frac{3}{2}

\frac{1}{2}

3. Cách xác định trọng tâm tam giác

Để xác định trọng tâm của một tam giác, chúng ta có thể thực hiện theo các bước sau:

Cách 1:

Tìm trung điểm M của cạnh BC sao cho MC = MB.
Nối đỉnh A với trung điểm M để tạo thành đường trung tuyến AM.
Lặp lại quy trình tương tự để xác định các đường trung tuyến còn lại.
Giao điểm của ba đường trung tuyến chính là điểm G, trọng tâm của tam giác ABC.

Cách 2:

Tìm trung điểm M của cạnh BC sao cho MC = MB.

Nối đỉnh A với trung điểm M để tạo thành đường trung tuyến AM.

A G = \frac{2}{3} A M

Theo tính chất của trọng tâm, điểm G chính là trọng tâm của tam giác ABC.

Cho tam giác ABC với AM, BN, CP lần lượt là ba đường trung tuyến xuất phát từ các đỉnh A, B, C. Giao điểm của ba đường trung tuyến này là điểm G, và G chính là trọng tâm của tam giác ABC.

Ta có tính chất:

$\overrightarrow{AG} = \dfrac{2}{3} \overrightarrow{AM} \Rightarrow AG = \dfrac{2}{3} AM$

\vec{A G} = \frac{2}{3} \vec{A M} \Rightarrow A G = \frac{2}{3} A M

$\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$

\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}

4. Trọng tâm của các hình học đặc biệt

A. Trọng tâm tam giác vuông

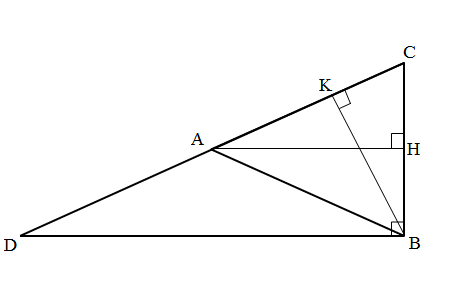
Tam giác ABC vuông tại B, từ B vẽ đường trung tuyến BA. Vì BA là đường trung tuyến của góc vuông, nên BA = 1/2 CD = AD = AC.

Do đó, tam giác ADB và tam giác ABC lần lượt cân tại A.

B. Trọng tâm tam giác cân

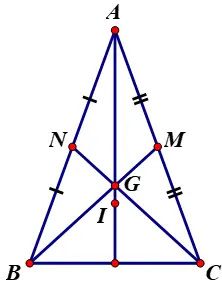
Cho tam giác ABC cân tại A, G là trọng tâm của tam giác ABC. Vì tam giác cân tại A, AG vừa là đường trung tuyến, vừa là đường cao và là đường phân giác của tam giác ABC.

Hệ quả:

$- \widehat{BAG} = \widehat{CAG}$

- \hat{B A G} = \hat{C A G}

- AG vuông góc với BC.

C. Trọng tâm tam giác đều

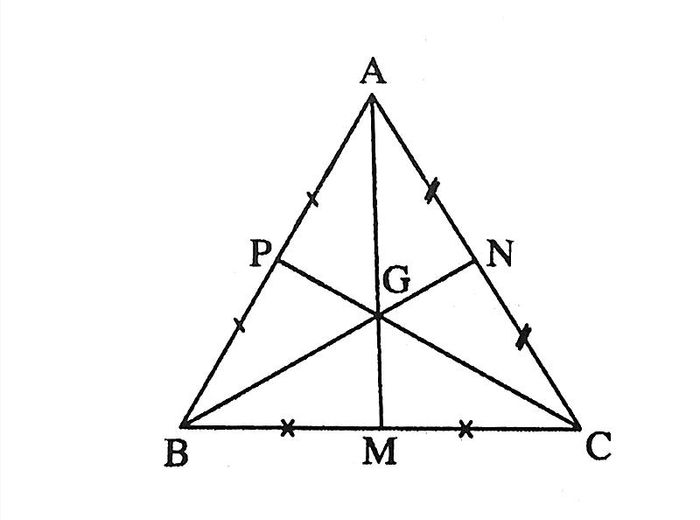
Cho tam giác ABC đều, G là giao điểm của ba đường trung tuyến. Theo tính chất của tam giác đều, G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

D. Trọng tâm tứ diện

Gọi G là trọng tâm của tứ diện ABCD.

Trọng tâm tứ diện là giao điểm của bốn đường thẳng nối từ đỉnh đến trọng tâm của tam giác đối diện.

5. Bài tập trọng tâm của tam giác

Bài tập 1: Cho tam giác ABC, trung tuyến BM = CN. BM cắt CN tại G. Chứng minh tam giác ABC cân tại A.

Lời giải:

Vì BM và CN là hai đường trung tuyến của tam giác, và BM giao CN tại G, ta có:

$\dfrac{BG}{BM} = \dfrac{CG}{CN} = \dfrac{2}{3}$

\frac{B G}{B M} = \frac{C G}{C N} = \frac{2}{3}

Do BM = CN, suy ra BG = CG và GN = GM.

$\Delta CGM$

Δ C G M

BG = CG

GN = GM

$\widehat{BGN} = \widehat{CGM}$

\hat{B G N} = \hat{C G M}

$\Delta$

Δ

$\Delta$

Δ

Suy ra: BN = CM (1)

Mà M và N lần lượt là trung điểm của AB và AC (2)

Từ (1) và (2), ta có AB = AC ⇒ Tam giác ABC cân tại A (đpcm).

Bài tập 2

Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.

Lời giải:

Vẽ hình:

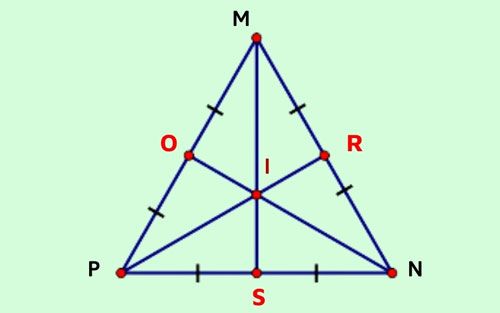
Gọi trung điểm của MN, MP, PN lần lượt là R, O, S.

Khi đó, MS, PR, NO đồng quy tại trọng tâm I.

Ta có ∆MNP đều, suy ra:

MS = PR = NO (1).

Vì I là trọng tâm của ∆MNP, theo tính chất đường trung tuyến:

MI = 2/3 MS, PI = 2/3 PR, NI = 2/3 NO (2).

Từ (1) và (2), suy ra GA = GB = GC.

Bài tập 3: Tam giác ABC có trung tuyến AD = 9cm và trọng tâm I. Tính độ dài đoạn AI?

Lời giải

Vẽ hình minh họa:

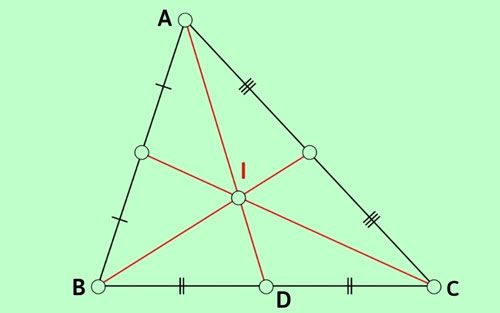
Vì I là trọng tâm của tam giác ABC và AD là đường trung tuyến, nên AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác).

Do đó: AI = (2/3) × 9 = 6 (cm).

Vậy đoạn AI có độ dài 6 cm.

Như vậy, với những kiến thức cơ bản và bài tập luyện tập trên, EduTOPS hy vọng bạn đọc đã có được sự hiểu biết vững chắc về trọng tâm. Hãy nắm vững các kiến thức này để giải quyết hiệu quả các bài tập hình học từ cơ bản đến nâng cao.