Toán Tiểu học: Khám phá công thức tính diện tích, chu vi và thể tích các hình học cơ bản dành cho học sinh

Toán Tiểu học: Công thức tính diện tích, chu vi, thể tích hình cơ bản Hệ thống đầy đủ các công thức tính chu vi, diện tích và thể tích của các hình học cơ bản, giúp học sinh nắm vững kiến thức Toán học một cách hiệu quả.

Nhờ đó, học sinh có thể dễ dàng nhận biết và áp dụng các công thức vào bài tập liên quan đến hình tam giác, hình tứ giác, hình vuông, hình chữ nhật, hình tròn, hình bình hành, hình thoi, hình nón, hình cầu, hình trụ, hình lập phương, hình thang, hình hộp chữ nhật và hình lăng trụ đứng. Điều này giúp các em học tốt phần Hình học. Mời các em cùng theo dõi bài viết chi tiết dưới đây của EduTOPS:

1. Công thức tính chu vi và diện tích hình chữ nhật

Công thức tính chu vi hình chữ nhật

Công thức: P = (a + b) x 2.

Để tính chu vi hình chữ nhật, ta cộng chiều dài với chiều rộng rồi nhân kết quả với 2 (cùng đơn vị đo).

Mở rộng: Nếu biết chu vi, ta có thể tìm cạnh chưa biết bằng cách lấy nửa chu vi (P : 2) trừ đi cạnh đã biết.

Công thức tính diện tích hình chữ nhật

Công thức: S = a x b.

Để tính diện tích hình chữ nhật, ta nhân chiều dài với chiều rộng (cùng đơn vị đo).

Mở rộng: Nếu biết diện tích, ta có thể tìm cạnh chưa biết bằng cách lấy diện tích chia cho cạnh đã biết.

2. Công thức tính chu vi và diện tích hình vuông

Công thức tính chu vi hình vuông

Công thức: P = a x 4

Để tính chu vi hình vuông, ta nhân độ dài một cạnh với 4.

Mở rộng: Nếu biết chu vi hình vuông, ta có thể tìm độ dài cạnh bằng cách lấy chu vi chia cho 4.

Công thức tính diện tích hình vuông

Công thức: S = a x a.

Để tính diện tích hình vuông, ta nhân độ dài một cạnh với chính nó.

Mở rộng: Nếu biết diện tích hình vuông, ta có thể tìm độ dài cạnh bằng cách nhẩm căn bậc hai của diện tích.

3. Công thức tính chu vi và diện tích hình bình hành

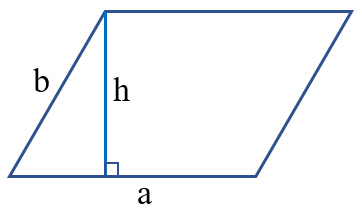
Công thức tính chu vi hình bình hành

Công thức: P = (a + b) x 2

Để tính chu vi hình bình hành, ta cộng hai cạnh kề nhau rồi nhân kết quả với 2 (cùng đơn vị đo).

Mở rộng: Nếu biết chu vi, ta có thể tìm cạnh chưa biết bằng cách lấy nửa chu vi (P : 2) trừ đi cạnh đã biết.

Công thức tính diện tích hình bình hành

Công thức: S = a x h

Để tính diện tích hình bình hành, ta nhân độ dài đáy với chiều cao (cùng đơn vị đo).

Mở rộng: Nếu biết diện tích hình bình hành, ta có thể tính:

• Độ dài đáy: a = S : h
• Chiều cao: h = S : a

4. Công thức tính chu vi và diện tích hình thoi

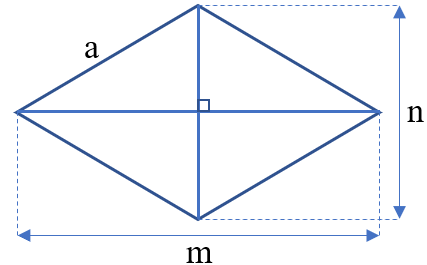
Công thức tính chu vi hình thoi

Công thức: P = a x 4

Để tính chu vi hình thoi, ta nhân độ dài một cạnh với 4.

Mở rộng: Nếu biết chu vi hình thoi, ta có thể tìm độ dài cạnh bằng cách lấy chu vi chia cho 4.

Công thức tính diện tích hình thoi

Để tính diện tích hình thoi, ta nhân độ dài hai đường chéo rồi chia kết quả cho 2 (cùng đơn vị đo).

5. Công thức tính chu vi và diện tích hình tam giác

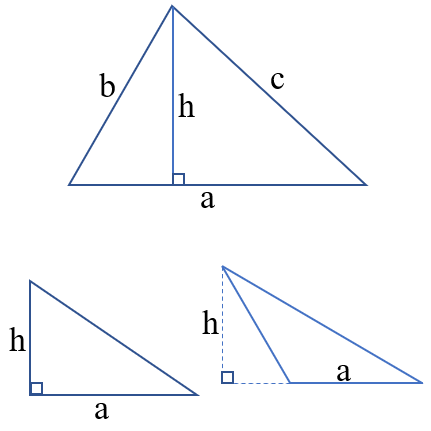
Công thức tính chu vi hình tam giác

Công thức: C = a + b + c

Để tính chu vi hình tam giác, ta cộng độ dài ba cạnh lại với nhau (cùng đơn vị đo).

Mở rộng: Nếu biết chu vi và hai cạnh của hình tam giác, ta có thể tìm cạnh còn lại bằng cách lấy chu vi trừ đi tổng hai cạnh đã biết: a = C - (b + c).

Công thức tính diện tích hình tam giác

Để tính diện tích hình tam giác, ta nhân độ dài đáy với chiều cao rồi chia kết quả cho 2 (cùng đơn vị đo).

Mở rộng: Nếu biết diện tích hình tam giác, ta có thể tính:

• Chiều cao: h = (S x 2) : a
• Cạnh đáy: a = (S x 2) : h

6. Công thức tính chu vi và diện tích hình tứ giác

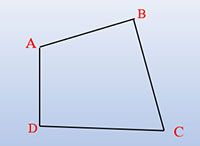
Công thức tính chu vi hình tứ giác

Công thức: P = a + b + c + d

Trong đó:

P là chu vi hình tứ giác
a, b, c, d lần lượt là độ dài các cạnh của tứ giác

Công thức tính diện tích hình tứ giác

Không có công thức chung để tính diện tích hình tứ giác. Tùy thuộc vào loại hình tứ giác cụ thể, chúng ta sẽ áp dụng các công thức tính diện tích khác nhau.

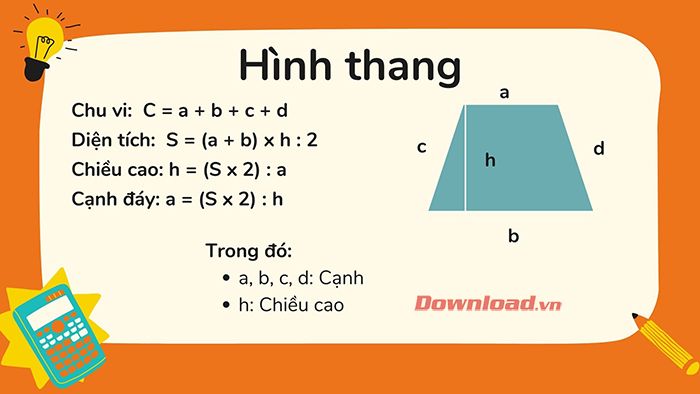
7. Tính chu vi và diện tích hình thang vuông, hình thang cân

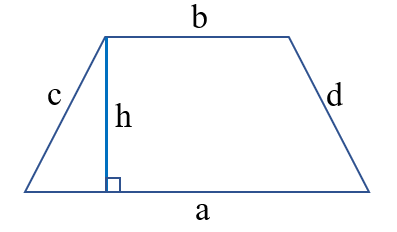
Hình thang vuông có một cạnh bên vuông góc với hai đáy, và cạnh bên đó chính là chiều cao. Diện tích hình thang vuông được tính tương tự như hình thang thường.

Hình thang cân có hai đường chéo bằng nhau, hai góc tù bằng nhau và hai góc nhọn bằng nhau.

Công thức tính chu vi hình thang

Công thức: C = a + b + c + d

Để tính chu vi hình thang, ta cộng độ dài tất cả các cạnh của hình thang lại với nhau (cùng đơn vị đo).

Mở rộng: Nếu biết chu vi và độ dài ba cạnh của hình thang, ta có thể tìm cạnh còn lại bằng cách lấy chu vi trừ đi tổng độ dài ba cạnh: a = C - (b + c + d).

Công thức tính diện tích hình thang

Để tính diện tích hình thang, ta cộng độ dài hai đáy, nhân với chiều cao, rồi chia kết quả cho 2 (cùng đơn vị đo).

Mở rộng: Nếu biết diện tích hình thang, ta có thể tính:

• Chiều cao: h = (S x 2) : (a + b)
• Cạnh đáy: a = (S x 2) : h - b

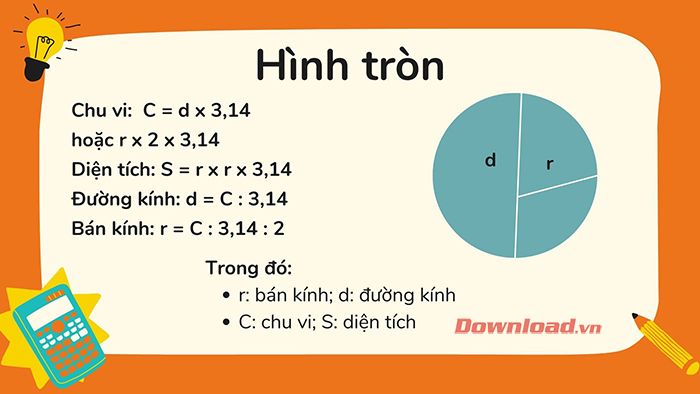
8. Công thức tính chu vi và diện tích hình tròn

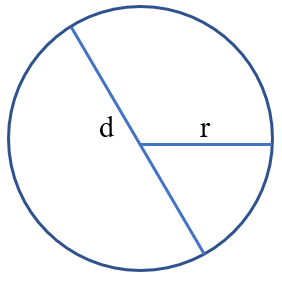
Công thức tính chu vi hình tròn

Công thức: C = d x 3,14
hoặc r x 2 x 3,14

Để tính chu vi hình tròn, ta nhân đường kính với số 3,14 (hoặc nhân bán kính với 2 rồi nhân với 3,14).

Mở rộng: Nếu biết chu vi hình tròn, ta có thể tính:

• Đường kính: d = C : 3,14
• Bán kính: r = C : 3,14 : 2

Công thức tính diện tích hình tròn

Công thức: r x r x 3,14

Để tính diện tích hình tròn, ta nhân bán kính với bán kính rồi nhân với số 3,14.

9. Công thức tính diện tích và thể tích hình lập phương

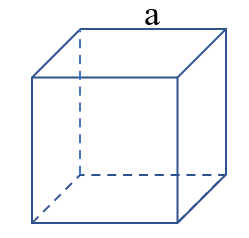
Tính diện tích xung quanh hình lập phương

Công thức: S_xq = S_m x 4

Để tính diện tích xung quanh, ta nhân diện tích một mặt của hình lập phương với 4.

Tính diện tích toàn phần hình lập phương

Công thức: S_tp = S_m x 6

Để tính diện tích toàn phần, ta nhân diện tích một mặt của hình lập phương với 6.

Tính thể tích hình lập phương

Công thức: V = a x a x a

Để tính thể tích hình lập phương, ta nhân độ dài cạnh với chính nó ba lần.

10. Công thức tính diện tích và thể tích hình hộp chữ nhật

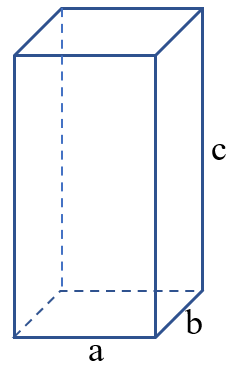
Tính diện tích xung quanh hình hộp chữ nhật

Công thức: S_xq = P x c

Để tính diện tích xung quanh hình hộp chữ nhật, ta nhân chu vi mặt đáy với chiều cao (cùng đơn vị đo).

Tính diện tích toàn phần hình hộp chữ nhật

Công thức: S_tp = S_xq + S_đ x 2

Để tính diện tích toàn phần hình hộp chữ nhật, ta cộng diện tích xung quanh với hai lần diện tích đáy (cùng đơn vị đo).

Tính thể tích hình hộp chữ nhật

Công thức: V = a x b x c

Để tính thể tích hình hộp chữ nhật, ta nhân chiều dài với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).

11. Công thức tính diện tích và thể tích hình nón

Công thức tính diện tích xung quanh hình nón

Diện tích xung quanh hình nón được tính bằng tích của hằng số Pi (π) nhân với bán kính đáy (r) và đường sinh (l). Đường sinh là khoảng cách từ mép đáy đến đỉnh hình nón.

Trong đó:

• Sxq: Diện tích xung quanh hình nón.
• π: Hằng số Pi (≈ 3,14).
• r: Bán kính đáy hình nón (r = d/2).
• l: Đường sinh của hình nón.

Công thức tính diện tích toàn phần hình nón

Diện tích toàn phần hình nón bằng tổng diện tích xung quanh và diện tích mặt đáy. Diện tích mặt đáy được tính theo công thức diện tích hình tròn: Sđ = π.r².

Công thức tính thể tích hình nón

Để tính thể tích hình nón, ta áp dụng công thức sau:

Trong đó:

• V: Thể tích hình nón.
• π: Hằng số Pi (≈ 3,14).
• r: Bán kính đáy hình nón.
• h: Chiều cao từ đỉnh đến tâm đáy.

12. Công thức tính diện tích và thể tích hình trụ

Công thức tính diện tích xung quanh hình trụ

S (xung quanh) = 2 x π x r x h

Trong đó:

• r: Bán kính đáy hình trụ.
• h: Chiều cao hình trụ.
• π = 3,14

Công thức tính diện tích toàn phần hình trụ

S (toàn phần) = 2 x π x r² + 2 x π x r x h = 2πr(r + h)

Trong đó:

• r: Bán kính đáy hình trụ.
• 2 x π x r x h: Diện tích xung quanh hình trụ.
• 2 x π x r²: Diện tích hai đáy hình trụ.

Công thức tính thể tích hình trụ

V = π x r² x h

Trong đó:

• r: Bán kính đáy hình trụ.
• h: Chiều cao hình trụ.

13. Công thức tính chu vi và diện tích hình cầu

Công thức tính diện tích mặt cầu

Công thức tính thể tích hình cầu

Trong đó:

• S là diện tích mặt cầu
• V là thể tích hình cầu
• r là bán kính mặt cầu/hình cầu
• d là đường kính mặt cầu/hình cầu

14. Thể tích hình lăng trụ đứng

Công thức tính thể tích hình lăng trụ đứng:

V = Sh

• Trong đó:
• S là diện tích mặt đáy
• h là chiều cao của lăng trụ