Mới nhất Ngữ văn IELTS TOEIC Từ vựng tiếng Anh Tiếng Anh giao tiếp Tiếng Anh THPT Kỹ năng tiếng Anh Ngôn ngữ khác

Nội dung bài viết

1. Khái niệm đường tròn ngoại tiếp tam giác
2. Tâm đường tròn ngoại tiếp tam giác là gì?
3. Tính chất đặc trưng của đường tròn ngoại tiếp
4. Các công thức tính bán kính đường tròn ngoại tiếp
5. Cách xác định tâm đường tròn ngoại tiếp tam giác
6. Phương trình đường tròn ngoại tiếp tam giác
7. Bán kính đường tròn ngoại tiếp tam giác
8. Bài tập về đường tròn ngoại tiếp tam giác
9. Bài tập tự luyện về tâm đường tròn ngoại tiếp tam giác

Tâm đường tròn ngoại tiếp tam giác: Lý thuyết cơ bản và các dạng bài tập thường gặp về đường tròn ngoại tiếp

Chia sẻ

Tâm đường tròn ngoại tiếp tam giác chính là điểm hội tụ của ba đường trung trực. Điểm này không chỉ là trung tâm cân đối mà còn là nơi khoảng cách đến ba đỉnh của tam giác đều bằng nhau, tạo nên một đường tròn duy nhất bao quanh cả ba đỉnh.

Dạng bài tập về tâm đường tròn ngoại tiếp tam giác là một trong những chủ đề trọng yếu trong chương trình Toán THCS, thường xuất hiện trong các kỳ thi vào lớp 10. Vậy làm thế nào để xác định tâm đường tròn ngoại tiếp và công thức tính bán kính là gì? Hãy cùng EduTOPS khám phá chi tiết qua bài viết dưới đây. Để mở rộng kiến thức Toán học, các em có thể tham khảo thêm các tài liệu như: chuyên đề Giải phương trình bậc hai chứa tham số, bài tập về hệ thức Vi-et và các ứng dụng thực tiễn.

1. Khái niệm đường tròn ngoại tiếp tam giác

Đường tròn ngoại tiếp tam giác được định nghĩa là đường tròn đi qua cả ba đỉnh của tam giác. Tâm của đường tròn này chính là điểm giao nhau của ba đường trung trực, tạo nên một trung tâm cân đối và hài hòa trong hình học.

2. Tâm đường tròn ngoại tiếp tam giác là gì?

Tâm đường tròn ngoại tiếp tam giác được xác định là giao điểm của ba đường trung trực (hoặc chỉ cần hai đường trung trực trong một số trường hợp đặc biệt).

3. Tính chất đặc trưng của đường tròn ngoại tiếp

- Mỗi tam giác, dù có hình dạng hay kích thước nào, đều chỉ tồn tại duy nhất một đường tròn ngoại tiếp.

- Tâm của đường tròn ngoại tiếp tam giác được xác định là điểm giao nhau của ba đường trung trực, tạo nên sự cân đối và hài hòa trong hình học.

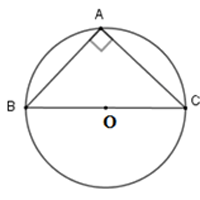
- Trong trường hợp tam giác vuông, tâm đường tròn ngoại tiếp nằm chính giữa cạnh huyền, thể hiện sự đối xứng đặc biệt.

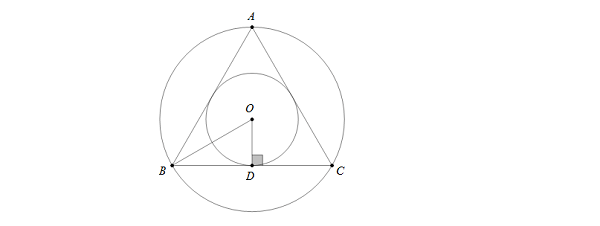
- Đối với tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp trùng khớp tại một điểm, phản ánh tính chất đối xứng hoàn hảo của hình dạng này.

4. Các công thức tính bán kính đường tròn ngoại tiếp

Công thức tính bán kính đường tròn ngoại tiếp tam giác được xác định bằng tích của ba cạnh tam giác chia cho bốn lần diện tích:

R = (a \times b \times c) : 4 S

$\mathrm{A}$

A

$r_{a}=\frac{2 S}{b+c-a}=\frac{S}{p-a}=p \cdot \tan \frac{A}{2}$

r_{a} = \frac{2 S}{b + c - a} = \frac{S}{p - a} = p \cdot \tan \frac{A}{2}

Công thức tính bán kính đường tròn ngoại tiếp của góc B

$r_{b}=\frac{2 S}{c+a-b}=\frac{S}{p-b}=p \cdot \tan \frac{B}{2}$

r_{b} = \frac{2 S}{c + a - b} = \frac{S}{p - b} = p \cdot \tan \frac{B}{2}

Công thức tính bán kính đường tròn ngoại tiếp của góc C

$r_{c}=\frac{2 S}{a+b-c}=\frac{S}{p-c}=p \cdot \tan \frac{C}{2}$

r_{c} = \frac{2 S}{a + b - c} = \frac{S}{p - c} = p \cdot \tan \frac{C}{2}

5. Cách xác định tâm đường tròn ngoại tiếp tam giác

Xác định tâm của đường tròn ngoại tiếp tứ giác

+ Tứ giác có bốn đỉnh cách đều một điểm. Điểm đó chính là tâm đường tròn ngoại tiếp tam giác.

+ Lưu ý: Quỹ tích các điểm nhìn đoạn thẳng AB dưới một góc vuông là đường tròn đường kính AB.

- Có hai phương pháp chính để xác định tâm đường tròn ngoại tiếp tam giác như sau:

- Cách 1:

+ Bước 1: Gọi I(x; y) là tâm của đường tròn ngoại tiếp tam giác ABC. Ta có IA = IB = IC = R.

$\left\{\begin{matrix} IA^2=IB^2\\ IA^2=IC^2 \end{matrix}\right.$

{\begin{matrix} I A^{2} = I B^{2} \\ I A^{2} = I C^{2} \end{matrix}

- Cách 2:

+ Bước 1: Viết phương trình đường trung trực của hai cạnh bất kỳ trong tam giác.

+ Bước 2: Tìm giao điểm của hai đường trung trực này, đó chính là tâm của đường tròn ngoại tiếp tam giác.

- Như vậy, tâm của đường tròn ngoại tiếp tam giác ABC cân tại A nằm trên đường cao AH.

Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền.

6. Phương trình đường tròn ngoại tiếp tam giác

Viết phương trình đường tròn ngoại tiếp tam giác ABC khi biết tọa độ ba đỉnh.

Để giải bài toán viết phương trình đường tròn ngoại tiếp tam giác, ta thực hiện theo bốn bước sau:

+ Bước 1: Thay tọa độ mỗi đỉnh vào phương trình với ẩn a, b, c (vì các đỉnh thuộc đường tròn ngoại tiếp nên tọa độ của chúng thỏa mãn phương trình).

+ Bước 2: Giải hệ phương trình để tìm các giá trị a, b, c.

+ Bước 3: Thay các giá trị a, b, c vừa tìm được vào phương trình tổng quát ban đầu => phương trình đường tròn ngoại tiếp tam giác cần tìm.

+ Bước 4: Do A, B, C ∈ C nên ta có hệ phương trình:

$\left\{\begin{matrix} x_{A}^{2} + y_{A}^{2} – 2ax_{A} – 2by_{A} + c = 0\\ x_{B}^{2} + y_{B}^{2} – 2ax_{B} – 2by_{B} + c = 0\\ x_{C}^{2} + y_{C}^{2} – 2ax_{C} – 2by_{C} + c = 0 \end{matrix}\right.$

{\begin{matrix} x_{A}^{2} + y_{A}^{2} - 2 a x_{A} - 2 b y_{A} + c = 0 \\ x_{B}^{2} + y_{B}^{2} - 2 a x_{B} - 2 b y_{B} + c = 0 \\ x_{C}^{2} + y_{C}^{2} - 2 a x_{C} - 2 b y_{C} + c = 0 \end{matrix}

=> Giải hệ phương trình trên để tìm các giá trị a, b, c.

Thay a, b, c vừa tìm được vào phương trình (C), ta có phương trình đường tròn ngoại tiếp tam giác cần tìm.

7. Bán kính đường tròn ngoại tiếp tam giác

Cho tam giác ABC

Gọi a, b, c lần lượt là độ dài các cạnh BC, AC, AB. S là diện tích tam giác ABC.

$R=\frac{a.b.c}{4S}$

R = \frac{a . b . c}{4 S}

8. Bài tập về đường tròn ngoại tiếp tam giác

Dạng 1: Viết phương trình đường tròn nội tiếp tam giác ABC khi biết tọa độ 3 đỉnh

Ví dụ: Viết phương trình đường tròn ngoại tiếp tam giác A, B, C biết A(-1; 2), B(6; 1), C(-2; 5).

Cách giải:

Gọi phương trình đường tròn ngoại tiếp tam giác ABC có dạng:

(C) x^{2} + y^{2} - 2 a x - 2 b y + c = 0

Do A, B, C cùng thuộc đường tròn nên thay tọa độ A, B, C lần lượt vào phương trình đường tròn (C) ta được hệ phương trình:

$\left\{\begin{matrix} 2a - 4b + c = -5\\ 12a + 2b - c = 37\\ 4a - 10b + c = -29 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} a = 3\\ b = 5\\ c = 9 \end{matrix}\right.$

{\begin{matrix} 2 a - 4 b + c = - 5 \\ 12 a + 2 b - c = 37 \\ 4 a - 10 b + c = - 29 \end{matrix} \Leftrightarrow {\begin{matrix} a = 3 \\ b = 5 \\ c = 9 \end{matrix}

Do đó, phương trình đường tròn ngoại tiếp tam giác ABC với tâm I(3; 5) và bán kính R = 5 là:

x^{2} + y^{2} - 6 x - 10 y + 9 = 0

(x - 3)^{2} + (y - 5)^{2} = 25

Dạng 2: Tìm tâm của đường tròn ngoại tiếp khi biết tọa độ ba đỉnh

Ví dụ: Cho tam giác ABC với A(1; 2), B(-1; 0), C(3; 2). Tìm tọa độ tâm của đường tròn ngoại tiếp tam giác ABC.

Hướng dẫn cách giải

Gọi I(x; y) là tâm của đường tròn ngoại tiếp tam giác ABC.

$\underset{IA}{\rightarrow} = (1 - x; 2 - y) \Rightarrow IA = \sqrt{(1 - x)^2 + (2 - y)^2}$

\underset{I A}{\to} = (1 - x; 2 - y) \Rightarrow I A = \sqrt{(1 - x)^{2} + (2 - y)^{2}}

$\underset{IB}{\rightarrow} = (-1 - x; -y) \Rightarrow IB = \sqrt{(1 - x)^2 + y^2}$

\underset{I B}{\to} = (- 1 - x; - y) \Rightarrow I B = \sqrt{(1 - x)^{2} + y^{2}}

$\underset{IC}{\rightarrow} = (3 - x; 2 - y) \Rightarrow IC = \sqrt{(3 - x)^2 + (2 - y)^2}$

\underset{I C}{\to} = (3 - x; 2 - y) \Rightarrow I C = \sqrt{(3 - x)^{2} + (2 - y)^{2}}

Vì I là tâm của đường tròn ngoại tiếp tam giác ABC nên ta có:

$IA = IB = IC \Leftrightarrow \left\{\begin{matrix} IA^2 = IB^2\\ IA^2 = IC^2 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} (1 - x)^2 + (2 - y)^2 = (-1 - x)^2 + y^2\\ (1 - x)^2 + (2 - y)^2 = (3 - x)^2 + (2 - y)^2 \end{matrix}\right.$

I A = I B = I C \Leftrightarrow {\begin{matrix} I A^{2} = I B^{2} \\ I A^{2} = I C^{2} \end{matrix} \Leftrightarrow {\begin{matrix} (1 - x)^{2} + (2 - y)^{2} = (- 1 - x)^{2} + y^{2} \\ (1 - x)^{2} + (2 - y)^{2} = (3 - x)^{2} + (2 - y)^{2} \end{matrix}

$\Leftrightarrow \left\{\begin{matrix} x + y = 1\\ x = 2 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 2\\ y = -1 \end{matrix}\right.$

\Leftrightarrow {\begin{matrix} x + y = 1 \\ x = 2 \end{matrix} \Leftrightarrow {\begin{matrix} x = 2 \\ y = - 1 \end{matrix}

Tọa độ tâm của đường tròn ngoại tiếp tam giác ABC được xác định là I(2; -1).

Dạng 3: Xác định bán kính đường tròn nội tiếp tam giác

Ví dụ: Tam giác ABC có các cạnh AB = 3, AC = 7, BC = 8. Hãy tính bán kính đường tròn ngoại tiếp tam giác ABC.

Phương pháp giải:

$p = \frac{AB + AC + BC}{2} = \frac{3 + 7 + 8}{2} = 9$

p = \frac{A B + A C + B C}{2} = \frac{3 + 7 + 8}{2} = 9

Áp dụng công thức Heron:

$S = \sqrt{p(p - AB)(p - AC)(p - BC)} = \sqrt{9(9 - 3)(9 - 7)(9 - 8)} = 6\sqrt{3}$

S = \sqrt{p (p - A B) (p - A C) (p - B C)} = \sqrt{9 (9 - 3) (9 - 7) (9 - 8)} = 6 \sqrt{3}

Bán kính đường tròn ngoại tiếp tam giác ABC được tính như sau:

$R = \frac{AB \cdot AC \cdot BC}{4S} = \frac{3 \cdot 7 \cdot 8}{4 \cdot 6\sqrt{3}}$

R = \frac{A B . A C . B C}{4 S} = \frac{3.7 .8}{4.6 \sqrt{3}}

Ví dụ 4: Cho tam giác MNP vuông tại N, với MN = 6cm, NP = 8cm. Hãy xác định bán kính đường tròn ngoại tiếp tam giác MNP.

Phương pháp giải:

Áp dụng định lý Pythagoras, ta có:

PQ = 1/2 MP, suy ra NQ = QM = QP = 5cm.

Gọi D là trung điểm của MP, khi đó ∆MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền MP.

Do đó, Q chính là tâm đường tròn ngoại tiếp ∆MNP.

Từ đó, đường tròn ngoại tiếp ∆MNP có tâm Q nằm trên cạnh huyền MP và bán kính R = MQ = 5cm.

Ví dụ 5: Cho tam giác ABC đều với độ dài cạnh là 6cm. Hãy xác định tâm và bán kính của đường tròn ngoại tiếp tam giác ABC.

Phương pháp giải:

Gọi D và E lần lượt là trung điểm của cạnh BC và AB. Giao điểm của AD và CE là O.

Vì tam giác ABC đều nên các đường trung tuyến đồng thời là đường cao, đường phân giác và đường trung trực của tam giác.

Từ đó, O chính là tâm đường tròn ngoại tiếp tam giác.

Trong ∆ABC, CE là đường trung tuyến nên cũng là đường cao.

Áp dụng định lý Pythagoras vào tam giác vuông AEC, ta có:

CE² = AC² – AE² = 6² – 3² = 27, suy ra CE = 3√3cm.

Vì O là trọng tâm của tam giác ABC nên CO = 2/3 CE = (2/3)3√3 = 2√3cm.

Kết luận: Tâm đường tròn ngoại tiếp tam giác ABC là trọng tâm O và bán kính là OC = 2√3cm.

Ví dụ 5: Cho tam giác MNP vuông tại N, với MN = 6cm và NP = 8cm. Hãy xác định bán kính đường tròn ngoại tiếp tam giác MNP.

Lời giải:

Đáp án cho bài tập 1

PQ = 1/2 MP, suy ra NQ = QM = QP = 5 cm.

P Q = 1 / 2 M P => N Q = Q M = Q P = 5 cm

M P => Δ M N P

M P . \Rightarrow Q

Δ MNP .

Δ MNP

R = MQ = 5 cm .

9. Bài tập tự luyện về tâm đường tròn ngoại tiếp tam giác

Bài 1: Các đường cao AD và BE của tam giác ABC cắt nhau tại H (góc C không phải góc vuông) và cắt đường tròn (O) ngoại tiếp tam giác ABC lần lượt tại I và K.

a) Chứng minh tứ giác CDHE nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác đó.

b) Chứng minh tam giác CIK là tam giác cân.

Bài 2: Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Ba đường cao của tam giác là AF, BE và CD cắt nhau tại H. Chứng minh tứ giác BDEC là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác.

Bài 3: Cho tam giác ABC vuông tại A với AB < AC, đường cao AH (H thuộc BC). Lấy điểm D sao cho H là trung điểm của BD. Gọi E là chân đường vuông góc hạ từ C xuống đường thẳng AD. Chứng minh tứ giác AHEC nội tiếp và xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác đó.

Bài 4:

Cho tam giác ABC cân tại A, với AB = AC, nội tiếp đường tròn tâm O. Các đường cao AQ, BE, CF cắt nhau tại một điểm.

a) Chứng minh rằng tứ giác AEHF là tứ giác nội tiếp, xác định tâm của đường tròn ngoại tiếp tứ giác đó.

b) Cho bán kính đường tròn tâm I là 2cm và góc BAC = 50⁰. Tính độ dài cung EHF của đường tròn tâm I và diện tích hình quạt tròn IEHF.

Bài 5: $\frac{R}{r}$

\frac{R}{r}

Bài 6: Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA và MB với đường tròn (O). Qua M kẻ cát tuyến MCD không đi qua tâm O, cắt đường tròn tại hai điểm C và D sao cho C nằm giữa M và D. Gọi I là trung điểm của dây CD. Khi đó, MAOIB có là ngũ giác nội tiếp hay không? Nếu có, hãy xác định tâm và bán kính của đường tròn đó.

Bài 7: Cho hình thang ABCD vuông tại A và D. Biết AB = 10cm, BC = 13cm, CD = 15cm. Chứng minh hình thang ABCD ngoại tiếp đường tròn, tìm bán kính đường tròn đó.

Bài 8: Cho tứ giác ABCD ngoại tiếp đường tròn, với các tia AB và CD cắt nhau tại E, các tia AD và BC cắt nhau tại F. Hãy chứng minh các đẳng thức sau: