Mới nhất Ngữ văn IELTS TOEIC Từ vựng tiếng Anh Tiếng Anh giao tiếp Tiếng Anh THPT Kỹ năng tiếng Anh Ngôn ngữ khác

Nội dung bài viết

1. Định nghĩa góc giữa hai mặt phẳng
2. Cách xác định góc giữa hai mặt phẳng
3. Công thức tính góc giữa hai mặt phẳng
4. Phương pháp tính góc giữa hai mặt phẳng
5. Bài tập áp dụng
6. Bài tập tự luyện

Góc giữa hai mặt phẳng: Khái niệm, phương pháp xác định và bài tập ứng dụng kèm đáp án chi tiết - Ôn tập Toán 11

Chia sẻ

Góc giữa hai mặt phẳng là một chủ đề trọng yếu trong chương trình Toán lớp 11 và 12, đóng vai trò nền tảng cho nhiều dạng bài tập phức tạp. Để thành thạo các bài toán liên quan, học sinh cần nắm vững lý thuyết cốt lõi, bao gồm định nghĩa, phương pháp xác định, và công thức tính góc giữa hai mặt phẳng.

Góc giữa hai mặt phẳng được hình thành bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Trong không gian ba chiều, góc này còn được biết đến với tên gọi góc khối, được tạo thành từ sự giao nhau của hai mặt phẳng. Dưới đây là tổng hợp kiến thức chi tiết về góc giữa hai mặt phẳng, kèm theo những ví dụ minh họa sinh động. Bên cạnh đó, bạn có thể tham khảo thêm về Công thức truy hồi để mở rộng hiểu biết.

1. Định nghĩa góc giữa hai mặt phẳng

- Khái niệm: Góc giữa hai mặt phẳng là gì? Đó là góc được hình thành bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Trong không gian ba chiều, góc giữa hai mặt phẳng còn được biết đến với tên gọi ‘góc khối’, tức là phần không gian được giới hạn bởi hai mặt phẳng. Góc này được xác định bằng góc tạo bởi hai đường thẳng nằm trên hai mặt phẳng, cùng vuông góc với giao tuyến của chúng.

- Tính chất: Từ định nghĩa trên, ta có thể rút ra các tính chất sau:

Góc giữa hai mặt phẳng song song bằng 0 độ.
Góc giữa hai mặt phẳng trùng nhau cũng bằng 0 độ.

2. Cách xác định góc giữa hai mặt phẳng

Để xác định chính xác góc giữa hai mặt phẳng, bạn có thể áp dụng các phương pháp sau đây:

Gọi P là mặt phẳng thứ nhất, Q là mặt phẳng thứ hai.

Trường hợp 1: Nếu hai mặt phẳng (P) và (Q) song song hoặc trùng nhau, góc giữa chúng sẽ bằng 0 độ.

Trường hợp 2: Nếu hai mặt phẳng (P) và (Q) không song song hoặc trùng nhau.

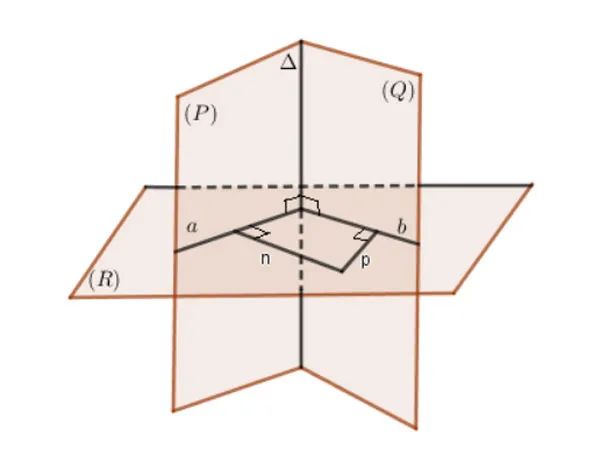
Cách 1: Dựng hai đường thẳng n và p lần lượt vuông góc với hai mặt phẳng (P) và (Q). Khi đó, góc giữa hai mặt phẳng (P) và (Q) chính là góc giữa hai đường thẳng n và p.

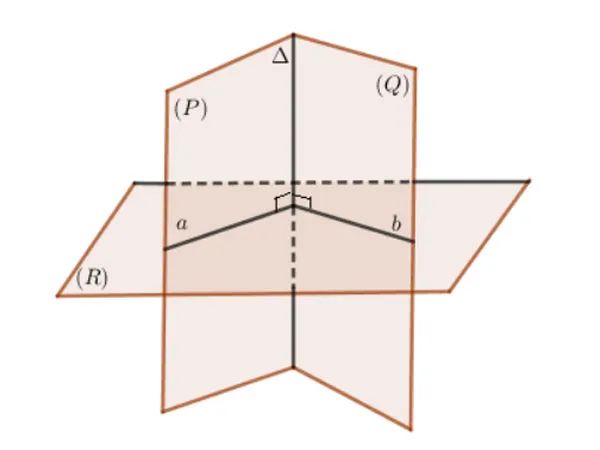
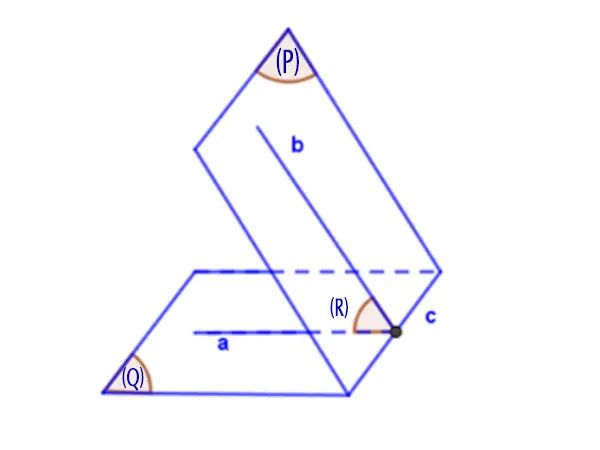
Cách 2: Để xác định góc giữa hai mặt phẳng, trước tiên bạn cần xác định giao tuyến Δ của hai mặt phẳng (P) và (Q). Sau đó, tìm một mặt phẳng (R) vuông góc với giao tuyến Δ và cắt hai mặt phẳng (P), (Q) tại các giao tuyến a và b.

⇒ Góc giữa hai mặt phẳng (P) và (Q) chính là góc giữa hai đường thẳng a và b.

3. Công thức tính góc giữa hai mặt phẳng

$\cos \varphi=|\cos \alpha|=\frac{\left|\vec{n}_{P} \cdot \vec{n}_{Q}\right|}{\left|\vec{n}_{P}\right| \cdot\left|\vec{n}_{Q}\right|}=\frac{\left|A_{1} A_{2}+B_{1} B_{2}+C_{1} C_{2}\right|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}} \cdot \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}} .$

\cos φ = | \cos α | = \frac{| {\vec{n}}_{P} \cdot {\vec{n}}_{Q} |}{| {\vec{n}}_{P} | \cdot | {\vec{n}}_{Q} |} = \frac{| A_{1} A_{2} + B_{1} B_{2} + C_{1} C_{2} |}{\sqrt{A_{1}^{2} + B_{1}^{2} + C_{1}^{2}} \cdot \sqrt{A_{2}^{2} + B_{2}^{2} + C_{2}^{2}}} .

4. Phương pháp tính góc giữa hai mặt phẳng

Có hai phương pháp chính để tính góc giữa hai mặt phẳng mà bạn có thể áp dụng:

Phương pháp 1: Sử dụng hệ thức lượng trong tam giác vuông, kết hợp với định lý hàm số sin và hàm số cos.

Ví dụ 1: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD với độ dài các cạnh đáy bằng a, và SA = SB = SC = SD = a. Hãy tính cos của góc giữa hai mặt phẳng (SAB) và (SAD).

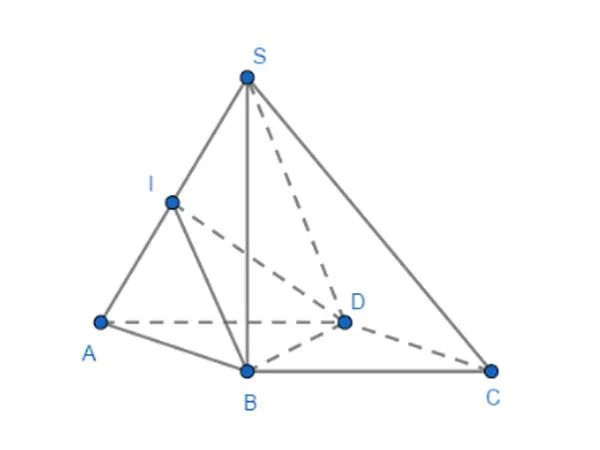
Phương pháp 2: Dựng mặt phẳng phụ (R) vuông góc với giao tuyến c, trong đó (Q) giao với (R) tạo thành đường thẳng a, và (P) giao với (R) tạo thành đường thẳng b.

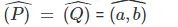
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh SA = a và vuông góc với mặt đáy. Hãy tính góc giữa hai mặt phẳng (SBC) và (ABCD), cũng như góc giữa mặt phẳng (SBD) và mặt phẳng (ABCD).

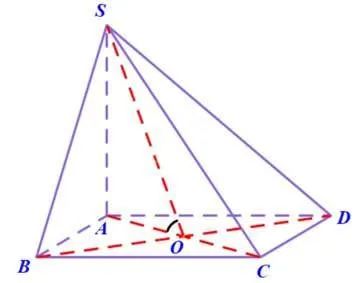
Gợi ý đáp án

Để tính góc giữa hai mặt phẳng (SBC) và (ABCD), chúng ta sẽ sử dụng phương pháp thứ hai.

- Giao tuyến của hai mặt phẳng (SBC) và (ABCD) chính là đường thẳng BC.

- Tiếp theo, chúng ta cần tìm (hoặc vẽ thêm nếu chưa có) một mặt phẳng vuông góc với giao tuyến BC. Nếu bạn nhận ra đó là mặt phẳng (SAB), thì rất tốt. Nếu chưa, hãy lưu ý hai điều sau:

+ Để có một mặt phẳng vuông góc với BC, cần tìm mặt phẳng chứa hai đường thẳng cắt nhau và cùng vuông góc với BC.

+ Đường thẳng BC vuông góc với những đường thẳng nào? (Chính là SA và AB).

- Sau khi xác định được mặt phẳng (SAB), chúng ta sẽ tìm giao tuyến của nó với hai mặt phẳng ban đầu, đó là các đường thẳng AB và SB.

- Cuối cùng, chúng ta tính góc giữa hai đường thẳng AB và SB, chính là góc SBA. Hãy tự tính xem góc này bằng bao nhiêu.

Để tính góc giữa hai mặt phẳng (SBD) và (ABCD), hãy thực hiện các bước tương tự như trên. Gợi ý, góc giữa hai mặt phẳng này chính bằng góc SOA.

5. Bài tập áp dụng

Câu 1: Xét tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh AC = a√2, và AC tạo với (P) một góc 60°. Hãy chọn khẳng định đúng trong các khẳng định sau?

A. (ABC) tạo với (P) góc 45°
B. BC tạo với (P) góc 30°
C. BC tạo với (P) góc 45°
D. BC tạo với (P) góc 60°

Câu 2: Cho tứ diện ABCD với AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây không đúng?

A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc ∠AIB
B. (BCD) ⊥ (AIB)
C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc ∠CBD
D. (ACD) ⊥ (AIB)
Câu 3: Cho hình chóp S.ABC có SA ⊥ (ABC) và AB ⊥ BC, gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?

A. Góc SBA.
B. Góc SCA.
C. Góc SCB.
D. Góc SIA.

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây không chính xác?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA
D. (SAC) ⊥ (SBD)

Câu 5: Cho hình lập phương ABCD.A1B1C1D1. Gọi α là góc giữa hai mặt phẳng (A1D1CB) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?

A. α = 45°
B. α = 30°
C. α = 60°
D. α = 90°

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và SA ⊥ (ABCD). Khẳng định nào sau đây không đúng?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. (SAC) ⊥ (SBD)
C. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
D. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA

Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc ∠ABC = 60°. Các cạnh SA; SB; SC đều bằng a(√3/2). Gọi φ là góc của hai mặt phẳng (SAC) và (ABCD). Giá trị tanφ bằng bao nhiêu?

A. 2√5
B. 3√5
C. 5√3
D. Đáp án khác

Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. AB = 2a; AD = DC = a. Cạnh bên SA vuông góc với đáy và SA = a√2. Chọn khẳng định sai trong các khẳng định sau?

A. (SBC) ⊥ (SAC)
B. Giao tuyến của (SAB) và (SCD) song song với AB
C. (SDC) tạo với (BCD) một góc 60°
D. (SBC) tạo với đáy một góc 45°

Câu 9: Cho hình hộp chữ nhật ABCD.A'B'C'D' với AB = AA’ = a; AD = 2a. Gọi α là góc giữa đường chéo A’C và mặt phẳng đáy ABCD. Hãy tính giá trị của α.

A. α ≈ 20°45'
B. α ≈ 24°5'
C. α ≈ 30°18'
D. α ≈ 25°48'

Câu 10: Cho hình lập phương ABCD.A'B'C'D'. Xét mặt phẳng (A’BD). Trong các mệnh đề sau, mệnh đề nào chính xác?

A. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa cạnh của hình lập phương là α với tanα = 1/√2.
B. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa cạnh của hình lập phương là α với tanα = 1/√3.
C. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa cạnh của hình lập phương phụ thuộc vào kích thước hình lập phương.
D. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa cạnh của hình lập phương bằng nhau.

Câu 11: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Hãy tính góc tạo bởi cạnh bên và mặt đáy.

A. 30°
B. 45°
C. 60°
D. 75°

Câu 12. Cho hình chóp tứ giác đều có cạnh đáy bằng a√2 và chiều cao bằng a√2/2. Tính góc giữa mặt bên và mặt đáy.

A. 30°
B. 45°
C. 60°
D. 75°

Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SCD) là bao nhiêu?

A. 30°
B. 45°
C. 90°
D. 60°

Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD); SA = x. Xác định giá trị của x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60°.

A. x = 3a/2
B. x = a/2
C. x = a
D. x = 2a

Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC). Gọi E và F lần lượt là trung điểm của AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là:

A. ∠CSF
B. ∠BSF
C. ∠BSE
D. ∠CSE

Câu 15: Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B và C, lấy các điểm D và E cùng phía so với (P) sao cho BD = a(√3/2) và CE = a√3. Hãy xác định góc giữa mặt phẳng (P) và mặt phẳng (ADE).

A. 30°
B. 60°
C. 90°
D. 45°

Câu 16. Trong các mệnh đề sau, mệnh đề nào chính xác?

A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước, chỉ tồn tại duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.

Câu 17. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước, chỉ có một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.

Câu 18: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.

Câu 19. Trong các mệnh đề sau, mệnh đề nào đúng?

Câu 20. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước, chỉ tồn tại duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Chỉ có một mặt phẳng duy nhất đi qua một điểm cho trước và vuông góc với hai mặt phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.

6. Bài tập tự luyện

Bài 1

a \sqrt{3}

1) Chứng minh rằng mặt phẳng (SBC) vuông góc với mặt phẳng (SAB) và mặt phẳng (SCD) vuông góc với mặt phẳng (SAD).

2) Tính góc tạo bởi mặt phẳng (SCD) và mặt phẳng (ABCD).

Bài 2: Hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và vuông góc với mặt phẳng (ABC).

1) Xác định vị trí của chân đường cao H kẻ từ đỉnh S của hình chóp.

2) Chứng minh rằng mặt phẳng (SBC) vuông góc với mặt phẳng (SAC).

3) Gọi I là trung điểm của cạnh SC, chứng minh rằng mặt phẳng (ABI) vuông góc với mặt phẳng (SBC).

Bài 3: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi I là trung điểm của cạnh BC.

1) Chứng minh rằng mặt phẳng (SBC) vuông góc với mặt phẳng (SAI).

2) Biết rằng góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) là 60 độ. Tính chiều cao SH của hình chóp.

Bài 4: Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a.

1) Tính độ dài đường cao của hình chóp.

2) Gọi M là trung điểm của SC. Chứng minh rằng mặt phẳng (MBD) vuông góc với mặt phẳng (SAC).

3) Tính góc tạo bởi mặt bên và mặt đáy của hình chóp.

Bài 5: Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, với AB = 2a,

AD = CD = a, cạnh SA vuông góc với đáy và SA = a.

1) Chứng minh rằng mặt phẳng (SAD) vuông góc với mặt phẳng (SCD) và mặt phẳng (SAC) vuông góc với mặt phẳng (SBC).

2) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD). Tính tan φ.

Bài 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA = a và SA vuông

góc với mặt phẳng (ABCD). Tính góc giữa mặt phẳng (SBC) và mặt phẳng (SCD).

Bài 7: $\widehat{\mathrm{ABC}}=60^{\circ}$

\hat{ABC} = 60^{\circ}

1) Chứng minh rằng mặt phẳng (SBD) vuông góc với mặt phẳng (ABCD).

2) Chứng minh rằng tam giác SBD là tam giác vuông.

Bài 8: Cho tam giác đều ABC cạnh a, I là trung điểm của BC và D là điểm đối xứng với A

$\mathrm{SD}=\frac{\mathrm{a} \sqrt{6}}{2}$

SD = \frac{a \sqrt{6}}{2}

1) Chứng minh rằng mặt phẳng (SAB) vuông góc với mặt phẳng (SAC).

2) Chứng minh rằng mặt phẳng (SBC) vuông góc với mặt phẳng (SAD).

Bài 9 $\mathrm{SD}=\frac{\mathrm{a} \sqrt{3}}{2}$

SD = \frac{a \sqrt{3}}{2}

1) Chứng minh rằng mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD) và SB vuông góc với BC.

2) Tính tang của góc tạo bởi mặt phẳng (SBD) và mặt phẳng (ABCD).

Bài 10: Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc nhau. Gọi I là trung điểm của AB.

1) Chứng minh rằng mặt phẳng (SAD) vuông góc với mặt phẳng (SAB).

2) Tính góc giữa đường thẳng SD và mặt phẳng (ABCD).

3) Gọi F là trung điểm của AD. Chứng minh rằng mặt phẳng (SCF) vuông góc với mặt phẳng (SID).

Bài 11

Cho hình chóp S.ABC, SA vuông góc với mặt phẳng (ABC).

a) Xác định góc giữa mặt phẳng (ABC) và mặt phẳng (SBC).

b) Giả sử tam giác ABC vuông tại B, hãy xác định góc giữa hai mặt phẳng (ABC) và (SBC).

Bài 12: Cho hình chóp tứ giác đều S.ABCD với đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = a. Tính cosin của góc giữa hai mặt phẳng (SAB) và (SAD).