Đường Trung Trực: Khái Niệm, Tính Chất Đặc Trưng và Bài Tập Ứng Dụng - Ôn Luyện Toán Lớp 7

Đường trung trực là một chủ đề toán học quan trọng trong chương trình Toán lớp 7 sách mới, đòi hỏi sự hiểu biết sâu sắc về cách nhận biết và chứng minh. Với độ phức tạp tương đối cao, nhiều học sinh gặp khó khăn khi tiếp cận. Hôm nay, EduTOPS mang đến cho bạn bộ tài liệu tổng hợp chi tiết nhất về đường trung trực, giúp bạn nắm vững kiến thức và vận dụng hiệu quả.

Tài liệu về đường trung trực bao gồm toàn bộ lý thuyết từ khái niệm, tính chất đặc trưng, phương pháp chứng minh, kèm theo các ví dụ minh họa sinh động và bài tập thực hành phong phú. Được biên soạn một cách chi tiết và dễ hiểu, tài liệu này giúp học sinh tiếp cận kiến thức một cách tự nhiên và hiệu quả. Ngoài ra, các em có thể tham khảo thêm các chủ đề liên quan như: cách vẽ hình chiếu, phương pháp chứng minh ba điểm thẳng hàng, bài tập về lũy thừa số hữu tỉ, và bài tập Nhân chia số hữu tỉ.

I. Khái niệm đường trung trực

Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng đó và vuông góc với nó.

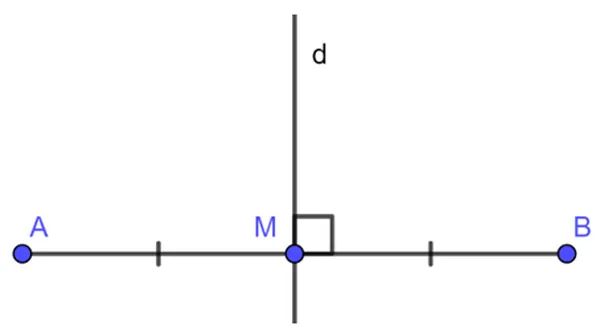
Định lý 1: Mọi điểm nằm trên đường trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng đó.

GT: d là đường trung trực của đoạn thẳng AB, M ∈ d

=> KL: MA = MB

Định lý 2:

Nếu một điểm cách đều hai đầu mút của một đoạn thẳng, thì điểm đó nằm trên đường trung trực của đoạn thẳng đó.

Nhận xét: Tập hợp tất cả các điểm cách đều hai đầu mút của một đoạn thẳng chính là đường trung trực của đoạn thẳng đó.

II. Tính chất đường trung trực

2.1. Đặc điểm của đường trung trực trong một đoạn thẳng

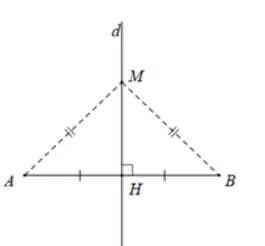
Trong hình minh họa, đường thẳng dd đóng vai trò là đường trung trực cho đoạn thẳng AB. Điều này cũng có nghĩa là điểm A và điểm B đối xứng với nhau qua đường thẳng d.

Nhận định:

Mọi điểm nằm trên đường trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng đó.

2.2. Đặc điểm của ba đường trung trực trong một tam giác

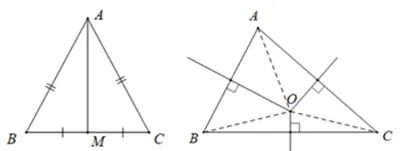
Trong hình vẽ, điểm O là nơi giao nhau của các đường trung trực trong tam giác ΔABC.

Tại điểm O, khoảng cách đến ba đỉnh A, B, và C là bằng nhau (OA = OB = OC). Điểm O này cũng chính là tâm của đường tròn ngoại tiếp tam giác ΔABC.

III. Phương pháp chứng minh đường trung trực trong chương trình lớp 7

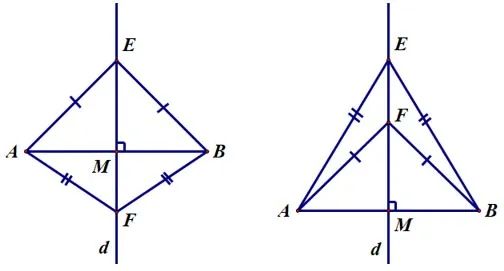
Để xác định đường thẳng d là đường trung trực của đoạn thẳng AB, chúng ta có thể áp dụng một trong hai phương pháp sau:

Phương pháp 1 (sử dụng định nghĩa): Chứng minh rằng đường thẳng d vuông góc với đoạn thẳng AB và đi qua trung điểm M của đoạn thẳng AB.

Phương pháp 2 (sử dụng tính chất): Chứng minh rằng đường thẳng d chứa hai điểm E và F, trong đó cả hai điểm này đều cách đều hai đầu mút A và B của đoạn thẳng.

IV. Các dạng toán thường gặp

Dạng 1: Chứng minh đường trung trực của một đoạn thẳng

- Phương pháp:

Để chứng minh đường thẳng dd là đường trung trực của đoạn thẳng AB, ta cần chứng minh dd đi qua hai điểm cách đều A và B hoặc áp dụng định nghĩa đường trung trực.

Dạng 2: Chứng minh hai đoạn thẳng bằng nhau

- Phương pháp:

Áp dụng định lý: “Điểm nằm trên đường trung trực của một đoạn thẳng sẽ cách đều hai đầu mút của đoạn thẳng đó.”

Dạng 3: Bài toán về giá trị nhỏ nhất

Phương pháp:

- Sử dụng tính chất đường trung trực để biến đổi độ dài một đoạn thẳng thành độ dài đoạn thẳng tương đương.

- Áp dụng bất đẳng thức tam giác để xác định giá trị nhỏ nhất.

Dạng 4: Xác định tâm đường tròn ngoại tiếp tam giác

Phương pháp:

Sử dụng tính chất giao điểm của ba đường trung trực trong tam giác.

Định lý: Ba đường trung trực của một tam giác đồng quy tại một điểm, điểm này cách đều ba đỉnh của tam giác.

Dạng 5: Bài toán liên quan đến đường trung trực đối với tam giác cân

Phương pháp:

Trong tam giác cân, đường trung trực của cạnh đáy không chỉ là đường trung tuyến mà còn đóng vai trò là đường phân giác ứng với cạnh đáy đó.

Dạng 6: Bài toán liên quan đến đường trung trực đối với tam giác vuông

Phương pháp:

Trong tam giác vuông, điểm giao nhau của các đường trung trực chính là trung điểm của cạnh huyền.

V. Cách xác định đường trung trực của một đoạn thẳng

Để xác định đường trung trực của một đoạn thẳng, hãy thực hiện lần lượt các bước sau:

1. Vẽ đoạn thẳng AB trên mặt phẳng.

2. Xác định trung điểm M của đoạn thẳng AB bằng cách chia AB thành hai phần có độ dài bằng nhau.

3. Dựng một đường thẳng đi qua trung điểm M và vuông góc với đoạn thẳng AB. Đường thẳng này chính là đường trung trực của AB.

4. Đường trung trực sẽ cắt đoạn thẳng AB tại trung điểm M và luôn tạo thành góc 90 độ với AB.

5. Kiểm tra tính chính xác bằng cách đo góc giữa đường trung trực và đoạn thẳng AB. Nếu góc đo được là 90 độ, đường trung trực đã được xác định đúng.

Phương pháp này đơn giản, dễ thực hiện và mang lại kết quả chính xác khi xác định đường trung trực của một đoạn thẳng.

VI. Một số câu hỏi thường gặp về đường trung trực

Số đường trung trực trong một đoạn thẳng?

Vì đường trung trực là đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng, và mỗi đoạn thẳng chỉ có một trung điểm duy nhất nên mỗi đoạn thẳng cũng chỉ có một đường trung trực duy nhất.

Cách viết phương trình đường trung trực của đoạn thẳng

Khi nghiên cứu về đường trung trực của đoạn thẳng, việc nắm vững cách viết phương trình của nó là rất quan trọng. Dưới đây là các bước cụ thể:

Bước 1. Xác định vectơ pháp tuyến của đường trung trực và một điểm mà nó đi qua.

Bước 2. Áp dụng định lý: “Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.” Tức là, nếu điểm M thuộc đường trung trực của AB thì MA = MB.

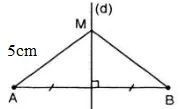
Ví dụ 1: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Nếu MA có độ dài 5cm thì độ dài MB bằng bao nhiêu?

Giải:

Vì điểm M nằm trên đường trung trực của đoạn thẳng AB nên theo định lý về tính chất của các điểm thuộc đường trung trực, ta có MA = MB. Do MA = 5cm (giả thiết), suy ra MB = 5cm.

Ví dụ 2: Vẽ một đoạn thẳng MN, sau đó sử dụng thước thẳng và compa để dựng đường trung trực của đoạn thẳng đó.

Ví dụ 3: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, cho đoạn thẳng MA có độ dài 5cm. Hỏi độ dài MB bằng bao nhiêu?

Ví dụ 3: 

Chứng minh đường thẳng PQ được vẽ như trong hình 43 đúng là đường trung trực của đoạn thẳng MN.

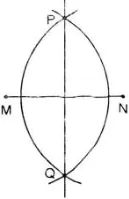
Giải:

Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại hai điểm P và Q.

Do đó, MP = NP và MQ = NQ.

⇒ P và Q cách đều hai đầu mút M và N của đoạn thẳng MN.

Theo định lý 2, P và Q thuộc đường trung trực của MN.

Vậy đường thẳng đi qua P và Q chính là đường trung trực của MN.

Kết luận: PQ là đường trung trực của MN.

Ví dụ 4

Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.

Gợi ý đáp án

Vì ΔABC cân tại A nên AB = AC.

⇒ Điểm A nằm trên đường trung trực của BC.

Vì ΔDBC cân tại D nên DB = DC.

⇒ Điểm D cũng nằm trên đường trung trực của BC.

Vì ΔEBC cân tại E nên EB = EC.

⇒ E nằm trên đường trung trực của BC.

Do đó, ba điểm A, D, E cùng thuộc đường trung trực của BC.

Vậy A, D, E thẳng hàng.

Ví dụ 5

Gọi O là giao điểm của ba đường trung trực trong ΔABC. Khi đó O là:

A. Điểm cách đều ba cạnh của ΔABC

B. Điểm cách đều ba đỉnh của ΔABC

C. Tâm đường tròn ngoại tiếp ΔABC

D. Đáp án B và C đúng

Gợi ý đáp án

Chọn đáp án D.

Ví dụ 6:

Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?

A. Tam giác vuông

B. Tam giác cân

C. Tam giác đều

D. Tam giác vuông cân

Gợi ý đáp án

Giả sử ΔABC có AM là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh ΔABC là tam giác cân. Thật vậy, vì AM là trung tuyến của ΔABC (giả thiết) ⇒ BM = MC (tính chất trung tuyến).

Vì AM là trung trực của BC ⇒ AM ⊥ BC.

Xét hai tam giác vuông ΔABM và ΔACM có:

BM = CM (chứng minh trên)

AM là cạnh chung

⇒ ΔABM = ΔACM (theo trường hợp hai cạnh góc vuông)

⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân tại A.

Chọn đáp án D.

Ví dụ 7

Cho đoạn thẳng AB thuộc nửa mặt phẳng bờ d. Xác định điểm M thuộc d sao cho M cách đều hai điểm A và B.

Gợi ý đáp án

Vẽ đường trung trực xy của đoạn thẳng AB.

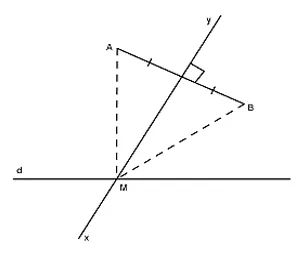
Giả sử xy cắt d tại điểm M, ta có: MA = MB.

+ Nếu AB ⊥ d thì xy // d, ta không xác định được điểm M.

+ Ngoài trường hợp AB ⊥ d, ta luôn xác định được điểm M và M là duy nhất.

Ví dụ 8

Cho tam giác ABC có AC > AB, phân giác AD. Trên AC lấy điểm E sao cho AE = AB. Chứng minh rằng AD vuông góc với BE.

Gợi ý đáp án

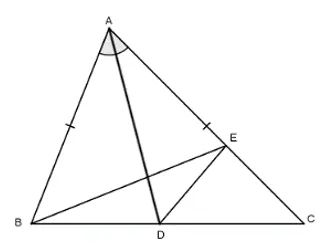
Ví dụ 9:

Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.

Gợi ý đáp án:

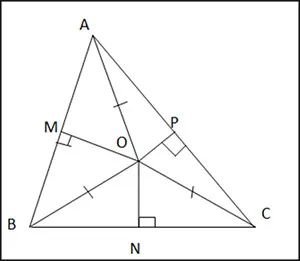
Xét ∆ MOB và ∆ MOA có:

MO chung

OB = OA

MB = MA (M là trung điểm của AB)

=> ∆ MOB = ∆ MOA (c.c.c)

=> OM ⊥ MB hay OM ⊥ AB

Tương tự ta có: ON ⊥ NB hay ON ⊥ BC

=> O là giao điểm của 2 đường trung trực OM và ON

mà P là trung điểm của AC

=> OP là đường trung trực của AC

=> OP ⊥ AC.

Ví dụ 10

Người ta muốn phục chế lại đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (hình 6). Làm thế nào để xác định bán kính bị vỡ của đĩa cổ này?

Gợi ý đáp án:

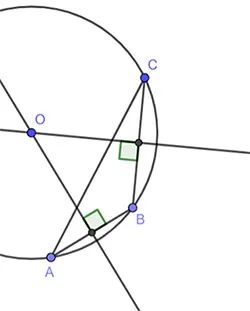
Lấy 3 điểm A, B, C bất kì thuộc cung tròn.

Xét tam giác ABC

Kẻ 2 đường trung trực của cạnh AB và BC. 2 đường trung trực cắt nhau tại điểm O

=> OA = OB = OC

=> O là tâm đường tròn qua ba điểm A, B, C.

=> OA, OB, OC là bán kính.

Vậy xác định được bán kính của đĩa cổ này là OA, OB, OC.

Ví dụ 11:

Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm ba đường trung trực của tam giác ABC.

Gợi ý đáp án

Do OA = OB nên O nằm trên đường trung trực của đoạn thẳng AB.

Do OB = OC nên O nằm trên đường trung trực của đoạn thẳng BC.

Tam giác ABC có O là giao điểm hai đường trung trực của đoạn thẳng AB và đoạn thẳng BC nên O là giao điểm ba đường trung trực của tam giác ABC.

Ví dụ 12 

Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.

Gợi ý đáp án

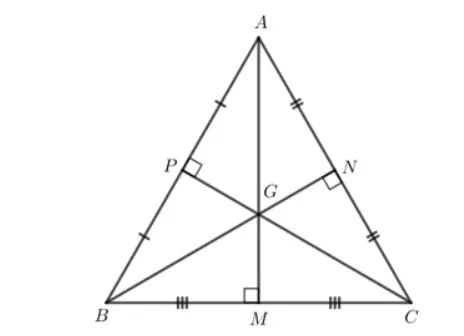
Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

Do G vừa là trọng tâm của tam giác và P là trung điểm của AB nên C, G, P thẳng hàng.

Do G là giao điểm ba đường trung trực của tam giác nên G nằm trên đường trung trực của cạnh AB, do đó C nằm trên đường trung trực của đoạn thẳng AB.

Suy ra CA = CB.

Thực hiện tương tự, ta thu được BA = BC.

Do đó AB = BC = CA.

Tam giác ABC có AB = BC = CA nên tam giác ABC đều.

Ví dụ 13

Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.

Gợi ý đáp án

Gọi M, N, P lần lượt là chân đường cao kẻ từ I đến BC, CA, AB.

Do I là giao điểm ba đường phân giác của tam giác ABC nên IM = IN = IP.

Do I là giao điểm ba đường trung trực của tam giác ABC nên I nằm trên đường trung trực của các cạnh BC, CA, AB.

Suy ra đường thẳng qua I, vuông góc với BC, CA, AB lần lượt là đường trung trực của các cạnh BC, CA, AB.

Do đó M, N, P lần lượt là đường trung trực của các cạnh BC, CA, AB.

Suy ra M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

Do AI là đường phân giác của góc BAC nên ∠BAI = ∠CAI.

Xét ∆PAI vuông tại P và ∆NAI vuông tại N có:

AI chung. ∠PAI = ∠NAI (chứng minh trên).

Suy ra ∆PAI = ∆NAI (cạnh huyền - góc nhọn).

Do đó PA = NA (2 cạnh tương ứng).

Mà P là trung điểm của AB nên PA = 1/2 BA; N là trung điểm của CA nên NA = 1/2 CA.

Suy ra AB = CA.

Thực hiện tương tự, ta thu được BA = BC.

Do đó AB = BC = CA.

Tam giác ABC có AB = BC = CA nên tam giác ABC đều.

VII. Bài tập trắc nghiệm về đường trung trực

Bài 1: Điểm C nằm trên đường trung trực của đoạn thẳng AB. Biết CA = 10 cm. Hỏi độ dài CB là bao nhiêu?

A. CB = 10 cm
B. CB = 20 cm
C. CB = 30 cm
D. CB = 40 cm

Bài 2: Nếu một tam giác có đường trung tuyến cũng là đường trung trực, thì tam giác đó thuộc loại nào?

A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân

Bài 3: Cho tam giác ABC cân tại A, với góc A = 40°. Đường trung trực của AB cắt BC tại D. Tính góc CAD.

A. 30°
B. 45°
C. 60°
D. 40°

Bài 4: Cho tam giác ABC vuông tại A, góc C = 30°. Đường trung trực của BC cắt AC tại M. Chọn câu đúng.

A. BM là đường trung tuyến của tam giác ABC
B. BM = AB
C. BM là phân giác của góc ABC
D. BM là đường trung trực của tam giác ABC

Bài 5: Cho đoạn thẳng AB với O là trung điểm. Trên hai nửa mặt phẳng đối nhau bờ AB, lấy hai điểm M và N sao cho MA = MB và NA = NB.

A. Đường thẳng MN đi qua O
B. Đường thẳng MN vuông góc với AB
C. Đường thẳng MN vuông góc với AB tại O
D. Đường thẳng MN song song với AB

Bài 6: Cho tam giác ABC vuông tại A, góc C = 30°. Đường trung trực của BC cắt AC tại M. Chọn câu đúng.

A. BM là đường trung tuyến của tam giác ABC
B. BM = AB
C. BM là phân giác của góc ABC
D. BM là đường trung trực của tam giác ABC

Bài 7:

Điểm C nằm trên đường trung trực của đoạn thẳng AB. Biết CA = 10 cm. Hỏi độ dài CB là bao nhiêu?

A. CB = 10 cm
B. CB = 20 cm
C. CB = 30 cm
D. CB = 40 cm

VIII. Bài tập tự luyện về đường trung trực

Bài 1: Cho tam giác ABC cân tại A. Hai trung tuyến BM và CN cắt nhau tại I. Hai tia phân giác trong của góc B và C cắt nhau tại O. Hai đường trung trực của hai cạnh AB và AC cắt nhau tại K.

a) Chứng minh rằng: BM = CN.

b) Chứng minh rằng OB = OC.

c) Chứng minh rằng các điểm A, O, I, K thẳng hàng.

Bài 2: Trên đường thẳng d là trung trực của đoạn thẳng AB, lấy hai điểm M và N nằm ở hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB.

b) Chứng minh rằng MN là tia phân giác của góc AMB.

Bài 3: Cho góc xOy = 50°, điểm A nằm trong góc xOy. Vẽ điểm M sao cho Ox là trung trực của đoạn AN, và vẽ điểm N sao cho Oy là trung trực của đoạn AM.

a) Chứng minh rằng: OM = ON.

Bài 4: Cho hai điểm A và B nằm trên cùng một mặt phẳng có bờ là đường thẳng d. Vẽ điểm C sao cho d là trung trực của đoạn thẳng BC, AC cắt d tại E. Trên d lấy điểm M bất kỳ.

a) So sánh MA + MB và AC.

b) Xác định vị trí của điểm M trên đường thẳng d sao cho tổng MA + MB đạt giá trị nhỏ nhất.

Bài 5: Cho tam giác ABC có góc A tù. Các đường trung trực của AB và AC cắt nhau tại O và lần lượt cắt BC tại D và E.

a) Xác định loại tam giác của ABD và ACE.

b) Đường tròn tâm O với bán kính OA sẽ đi qua những điểm nào trong hình vẽ?

Bài 6: Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường trung trực của cạnh AC, cắt BC tại I và cắt AC tại E.

a) Chứng minh rằng IA = IB = IC.

b) Gọi M là trung điểm của đoạn AI, chứng minh rằng MH = ME.

c) BE cắt AI tại N, tính tỉ số giữa đoạn MN và AI.

Bài 7: Cho bốn điểm A, B, C, D phân biệt. Với điều kiện nào thì đường thẳng AC trở thành đường trung trực của đoạn thẳng BD?

Bài 8: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Biết MA = 5 cm. Hỏi độ dài MB bằng bao nhiêu?

Bài 9: Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh rằng ∆AMN = ∆BMN.

Bài 10: Cho ba tam giác ABC, DBC, EBC có chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.

Bài 11: Cho tam giác ABC cân tại A. Đường trung trực của AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.

Bài 12: Cho tam giác ABC cân tại A, có góc A = 40°. Đường trung trực của AB cắt BC tại D. Tính góc CAD.

Bài 13: Cho tam giác ABC cân tại A. Đường trung trực của AC cắt AB tại D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.