Tam giác đều: Khám phá công thức tính diện tích và những đặc điểm hình học nổi bật

Chia sẻ

Tam giác đều là hình học đặc biệt với ba cạnh có độ dài bằng nhau và ba góc nội tại đều bằng 60°. Đây là một trong những đa giác đều cơ bản nhất, mang vẻ đẹp cân đối và hoàn hảo trong toán học.

Bạn đã bao giờ tự hỏi tính chất độc đáo của tam giác đều là gì? Làm thế nào để tính đường cao và diện tích của nó một cách chính xác? Hãy cùng EduTOPS khám phá chi tiết qua bài viết dưới đây, nơi chúng tôi mang đến những kiến thức bổ ích dành cho cả giáo viên và học sinh.

1. Tam giác đều là gì?

Tam giác đều là hình học đặc biệt với ba cạnh có độ dài bằng nhau và ba góc nội tại đều bằng 60°. Đây là một trong những đa giác đều cơ bản nhất, mang vẻ đẹp cân đối và hoàn hảo trong toán học.

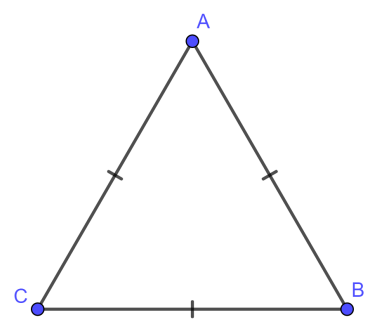
Trong tam giác ABC đều, ta có AB = AC = BC, thể hiện sự đồng nhất và cân bằng tuyệt đối giữa các cạnh.

Hệ quả:

Trong một tam giác đều, mỗi góc đều có giá trị bằng 60°, tạo nên sự hài hòa và đối xứng hoàn hảo.
Nếu một tam giác có ba góc bằng nhau, đó chính là tam giác đều, thể hiện sự cân bằng tuyệt đối.
Nếu một tam giác cân có một góc bằng 60°, nó sẽ trở thành tam giác đều, khẳng định tính chất độc đáo của hình học này.

2. Tính chất của tam giác đều

Tam giác đều sở hữu năm tính chất đặc trưng, bao gồm:

Trong một tam giác đều, mỗi góc đều có giá trị bằng 60°. (Tam giác ABC đều ∠A = ∠B = ∠C = 60°.)
Nếu một tam giác có ba góc bằng nhau, đó chính là tam giác đều. (∠A = ∠B = ∠C thì tam giác ABC là tam giác đều.)
Nếu một tam giác cân có một góc bằng 60°, nó sẽ trở thành tam giác đều.
Trong tam giác đều, đường trung tuyến đồng thời là đường cao và đường phân giác của tam giác đó.
Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A. Khi đó, AD cũng là đường cao và đường phân giác của tam giác ABC.

Những tính chất này đóng vai trò quan trọng trong việc giải các bài tập hình học. Hãy ghi nhớ kỹ năm tính chất của tam giác đều để áp dụng một cách hiệu quả và chính xác trong quá trình học tập.

3. Diện tích tam giác đều

Công thức tính diện tích của tam giác đều

S = a^{2} . \frac{\sqrt{3}}{4}

4. Dấu hiệu nhận biết của tam giác đều

Nếu tam giác đều có năm tính chất đặc trưng, thì dấu hiệu nhận biết của nó chỉ gồm bốn đặc điểm sau:

Tam giác có ba cạnh bằng nhau là tam giác đều.
Tam giác có ba góc bằng nhau là tam giác đều.
Tam giác cân có một góc bằng 60° là tam giác đều.
Tam giác có hai góc bằng 60 độ là tam giác đều.

5. Bài tập tam giác đều

Câu 1: Cho tam giác đều ABC có độ dài cạnh AB bằng 3 cm. Hãy tính đường cao và diện tích của tam giác đều này.

Câu 2: Cho tam giác đều ABC với cạnh AB = 5 cm. Hỏi chu vi của tam giác đều này bằng bao nhiêu?

Trên đây là toàn bộ kiến thức về tam giác đều. Hy vọng rằng qua bài viết này, các bạn học sinh sẽ củng cố và nắm vững kiến thức nền tảng, từ đó vận dụng hiệu quả vào việc giải quyết các bài tập liên quan. Đừng quên tham khảo thêm về đường cao trong tam giác cân để mở rộng hiểu biết của mình.