Khám phá các trường hợp bằng nhau của tam giác qua bài tập Hình học lớp 7 - Kiến thức và ứng dụng chi tiết

Các trường hợp bằng nhau của tam giác là một chủ đề quan trọng trong Hình học, bao gồm toàn bộ kiến thức từ khái niệm cơ bản đến các trường hợp cụ thể, kèm theo ví dụ minh họa sinh động và bài tập tự luyện đa dạng. Phần này không chỉ giúp học sinh nắm vững lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề thông qua các bài tập được thiết kế khoa học.

EduTOPS mang đến một bộ sưu tập các bài tập về các trường hợp bằng nhau của tam giác, bao gồm cả bài tập có đáp án và bài tập tự luyện. Những bài tập này được biên soạn với nhiều mức độ khó khác nhau, từ cơ bản đến nâng cao, giúp học sinh rèn luyện tư duy logic và hệ thống hóa kiến thức một cách hiệu quả. Qua đó, học sinh sẽ tự tin hơn khi đối mặt với các kỳ thi quan trọng, đồng thời phát triển khả năng giải quyết các dạng toán thường gặp trong chương trình học.

I. Mục tiêu

Sau khi hoàn thành chuyên đề này, học sinh sẽ đạt được những khả năng sau:

1. Vận dụng thành thạo các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau; Nắm vững các bước chứng minh hai đoạn thẳng hoặc hai góc bằng nhau; Biết cách vẽ thêm đường phụ nhằm tạo ra hai tam giác bằng nhau, từ đó giải quyết các bài toán phức tạp.

2. Hiểu rõ quy trình phân tích bài toán, từ đó tìm ra hướng chứng minh hợp lý và hiệu quả.

3. Phát triển kỹ năng vận dụng kiến thức đã học để giải quyết các bài toán hình học một cách sáng tạo và logic.

II. Các tài liệu hỗ trợ

- Sách Bài tập nâng cao và một số chuyên đề toán 7, cung cấp các dạng bài tập phong phú và chuyên sâu.

- Tài liệu Hình học nâng cao THCS, giúp học sinh khám phá sâu hơn về các khái niệm hình học phức tạp.

- Cuốn Vẽ thêm yếu tố phụ để giải các bài toán hình học 7, hướng dẫn chi tiết cách tiếp cận và giải quyết bài toán thông qua việc vẽ thêm các yếu tố phụ.

- Sách Bồi dưỡng toán 7, tập trung vào việc củng cố kiến thức và phát triển kỹ năng giải toán cho học sinh.

- Tài liệu Nâng cao và phát triển toán 7, mang đến các bài toán đa dạng và thử thách, giúp học sinh rèn luyện tư duy logic và sáng tạo.

III. Các trường hợp bằng nhau của hai tam giác

1. Kiến thức cần nhớ

Chúng ta đã biết rằng nếu hai tam giác bằng nhau, các cặp cạnh tương ứng và các cặp góc tương ứng cũng sẽ bằng nhau. Đây chính là lợi ích quan trọng của việc chứng minh hai tam giác bằng nhau trong hình học.

*. Các bước chứng minh hai đoạn thẳng hoặc hai góc bằng nhau thường được thực hiện như sau:

- Xác định xem hai đoạn thẳng (hoặc hai góc) đó thuộc về hai tam giác nào.

- Chứng minh hai tam giác đó bằng nhau.

- Từ đó suy ra hai cạnh (hoặc hai góc) tương ứng bằng nhau.

*. Để tạo ra hai tam giác bằng nhau, đôi khi cần vẽ thêm các yếu tố phụ bằng nhiều cách khác nhau:

- Nối hai cạnh có sẵn trên hình để tạo thành một cạnh chung của hai tam giác.

- Trên một tia cho trước, đặt một đoạn thẳng có độ dài bằng một đoạn thẳng khác.

- Từ một điểm cho trước, vẽ một đường thẳng song song với một đoạn thẳng đã có.

- Từ một điểm cho trước, vẽ một đường thẳng vuông góc với một đoạn thẳng đã có.

Ngoài ra, còn nhiều phương pháp khác mà chúng ta có thể tích lũy được thông qua kinh nghiệm giải nhiều bài toán khác nhau.

2. Các trường hợp bằng nhau của tam giác

a) Trường hợp 1: cạnh – cạnh – cạnh (c.c.c):

a) Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

b) Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

c) Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

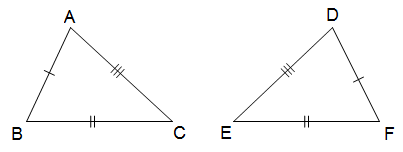
AB = DF (gt)

AC = DE (gt)

BC = EF (gt)

Suy ra ∆ABC = ∆DFE (c - c - c)

b) Trường hợp 2: cạnh – góc – cạnh:

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

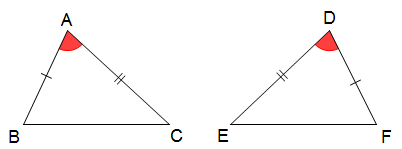
+ Xét ∆ABC và ∆DFE có:

AB = DF (gt)

AC = DE (giả thiết)

Từ đó suy ra ∆ABC = ∆DFE (cạnh - góc - cạnh)

Lưu ý: Để kết luận hai tam giác bằng nhau, cặp góc bằng nhau phải nằm giữa hai cặp cạnh tương ứng bằng nhau.

c) Trường hợp 3: góc – cạnh – góc:

Nếu một cạnh và hai góc kề của tam giác này bằng với một cạnh và hai góc kề của tam giác kia, thì hai tam giác đó bằng nhau.

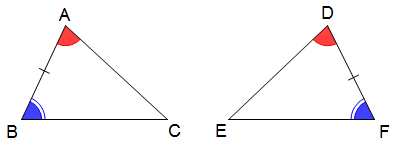
+ Xét ∆ABC và ∆DFE có:

AB = DF (giả thiết)

Từ đó suy ra ∆ABC = ∆DFE (góc - cạnh - góc)

Lưu ý:

- Để kết luận hai tam giác bằng nhau, cặp cạnh bằng nhau phải là cạnh tạo nên hai cặp góc tương ứng bằng nhau.

- Sau khi chứng minh hai tam giác bằng nhau, ta có thể suy ra các yếu tố tương ứng còn lại cũng bằng nhau.

IV. Các trường hợp bằng nhau của hai tam giác vuông

* Trường hợp cạnh góc vuông - cạnh góc vuông (cgv - cgv): Nếu hai cạnh góc vuông của tam giác vuông này tương ứng bằng hai cạnh góc vuông của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.

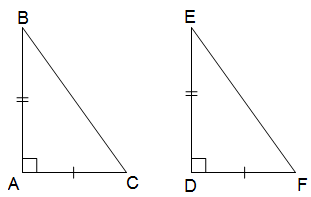
* Trường hợp cạnh góc vuông - góc nhọn (cgv - gn): Nếu một cạnh góc vuông và một góc nhọn kề cạnh đó của tam giác vuông này bằng với một cạnh góc vuông và một góc nhọn kề cạnh tương ứng của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.

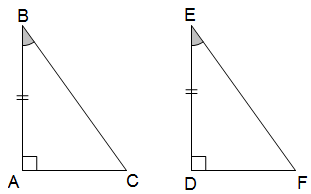
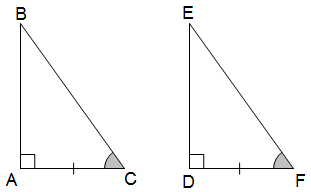
* Trường hợp cạnh huyền - góc nhọn (ch - gn): Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau.

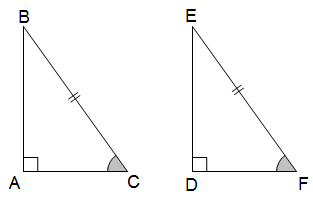
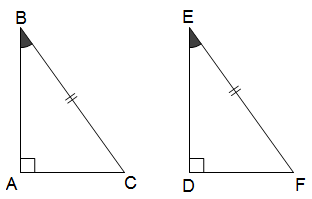
V. Ứng dụng các trường hợp bằng nhau của tam giác

Các trường hợp bằng nhau của tam giác thường được áp dụng để:

- Chứng minh: hai tam giác bằng nhau, hai đoạn thẳng có độ dài bằng nhau, hai góc có số đo bằng nhau; hai đường thẳng vuông góc hoặc song song; ba điểm nằm trên cùng một đường thẳng; ...

- Tính toán: độ dài các đoạn thẳng; số đo của các góc; chu vi và diện tích của các hình; ...

- So sánh: độ dài giữa các đoạn thẳng; số đo giữa các góc; ...

VI. Bài tập về hai tam giác bằng nhau

Bài 1: Cho tam giác ABC, với M là trung điểm của BC và N là một điểm nằm trong tam giác sao cho NB = NC.

Chứng minh rằng: ∆NMB = ∆NMC.

Bài 2: Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: ∆ABE = ∆ACE.

Bài 3: Cho tam giác ABC có góc A = 40°, AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 4: Cho tam giác ABC có AB = AC. Các điểm D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.

a. Chứng minh rằng góc EAB = góc DAC.

b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.

c. Giả sử góc DAE = 60°. Tính các góc còn lại của tam giác DAE.

Bài 5: Cho tam giác ABC có góc A = 90°. Vẽ AD ⊥ AB (D, C nằm khác phía đối với AB) và AD = AB. Vẽ AE ⊥ AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.

Bài 6: Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:

a. ∆ABE = ∆ACE.

b. AE là đường trung trực của đoạn thẳng BC.

Bài 7: Cho tam giác ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

a. ∆BDF = ∆EDC.

b. Chứng minh rằng BF = EC.

c. Chứng minh ba điểm F, D, E thẳng hàng.

d. Chứng minh AD vuông góc với FC.

Bài 8. Cho góc nhọn xOy. Trên tia Ox, lấy hai điểm A và C. Trên tia Oy, lấy hai điểm B và D sao cho OA = OB và OC = OD. (A nằm giữa O và C; B nằm giữa O và D).

a. Chứng minh rằng ∆OAD = ∆OBC.

b. So sánh hai góc CAD và CBD.

Bài 9. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC, lấy điểm D sao cho AD = AC.

a. Chứng minh rằng ΔABC = ΔABD.

b. Trên tia đối của tia AB, lấy điểm M. Chứng minh rằng ΔMBD = ΔMBC.

Bài 10. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kỳ. Chứng minh:

a. Chứng minh rằng ΔAOI = ΔBOI.

b. Chứng minh AB vuông góc với OI.

Bài 11. Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a. Chứng minh rằng AC song song với BE.

b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh ba điểm I, M, K thẳng hàng.

Bài 12: Cho tam giác ABC, với M là trung điểm của BC và N là một điểm nằm trong tam giác sao cho NB = NC. Chứng minh rằng: ∆NMB = ∆NMC.

Bài 13. Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: ∆ABE = ∆ACE.

Bài 14. Cho tam giác ABC có góc A = 40°, AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 15. Cho tam giác ABC (AB < AC) có AM là phân giác của góc A (M thuộc BC). Trên AC lấy điểm D sao cho AD = AB.

a. Chứng minh rằng BM = MD.

b. Gọi K là giao điểm của AB và DM. Chứng minh rằng ∆DAK = ∆BAC.

Bài 16. Cho tam giác ABC vuông tại C, có góc A bằng 60°. Tia phân giác của góc BAC cắt BC tại E. Kẻ EK vuông góc với AB (K thuộc AB), kẻ BD vuông góc với AE (D thuộc AE). Chứng minh:

a. AK = KB.

b. AD = BC.

Bài 17. Cho tam giác ABC. Qua A kẻ đường thẳng song song với BC, qua C kẻ đường thẳng song song với AB. Hai đường thẳng này cắt nhau tại D.

a. Chứng minh rằng ∆ABC = ∆ADC.

b. Chứng minh rằng ∆ADB = ∆CBD.

c. Gọi O là giao điểm của AC và BD. Chứng minh rằng ∆ABO = ∆COD.

Bài 18. Cho góc xAy khác góc bẹt. Gọi AD là tia phân giác của góc xAy. Qua D kẻ đường thẳng vuông góc với Ay, cắt Ay tại C và cắt Ax tại E. Qua D kẻ đường thẳng vuông góc với Ax, cắt Ax tại B và cắt Ay tại H. Chứng minh:

a. ∆ABD = ∆ACD.

b. DDBE = DDCH

c. DABH = DACE

Bài 19. Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và D. Trên tia Oy lấy hai điểm C và E sao cho OD = OE và OA = OB.

a. Chứng minh DODC = DOBE

b. Gọi A là giao điểm của BE và CD. Chứng minh DAOB = DAOC

c. Chứng minh BC vuông góc với OA

Bài 20 : Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Lấy E trên cạnh BC sao cho BE = AB.

a) Chứng minh : Δ ABD = Δ EBD.

b) Tia ED cắt BA tại M. Chứng minh : EC = AM

c) Nối AE. Chứng minh : góc AEC = góc EAM.

Bài 21: Cho tam giác ABC vuông góc tại A có góc B = 53⁰.

a) Tính góc C.

b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh : ΔBEA = ΔBED.

c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. Chứng minh : ΔBHF = ΔBHC.

d) Chứng minh: ΔBAC = ΔBDF và D, E, F thẳng hàng.

Bài 22: Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IH vuông góc với AB tại H và IK vuông góc với AC tại K.

a/ Chứng minh rằng: BH = CK.

b/ Chứng minh tứ giác AHIK nội tiếp đường tròn và xác định tâm của đường tròn đó.